Time-evolution with time-independent $H$

(Set $\hbar=1$ in the following). In this case, the initial value problem

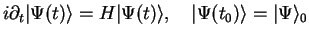$$i \partial_t \vert\Psi(t)\rangle = H\vert\Psi(t)\rangle,\quad \vert\Psi(t_0)\rangle = \vert\Psi\rangle_0$$ (1.6)

is formally solved as

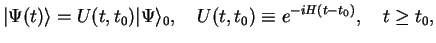$$\vert\Psi(t)\rangle = U(t,t_0)\vert\Psi\rangle_0,\quad U(t,t_0)\equiv e^{-i H (t-t_0)},\quad t\ge t_0,$$ (1.7)

where we introduced the time-evolution operator $U(t,t_0)$ as the exponential of the operator $-iH(t-t_0)$ by the power series

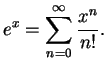$$e^x = \sum_{n=0}^{\infty} \frac{x^n}{n!}.$$ (1.8)

Things are simple, however, when we use the solutions of the stationary Schrödinger equation

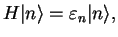$$H\vert n\rangle = \varepsilon_n \vert n\rangle,$$ (1.9)

where the eigenstates $\vert n\rangle$ form a complete basis and one has

$$\langle n \vert\Psi(t)\rangle = \sum_m \langle n\vert e^{-i H (t-t_0)}\vert m \rangle \langle m \vert\Psi\rangle_0$$ (1.10)

$$= \sum_m \langle n\vert m \rangle e^{-i \varepsilon_m (t-t_0)} \langle m \vert\Psi\rangle_0$$

$$= \sum_m \delta_{nm} e^{-i \varepsilon_m (t-t_0)} \langle m \vert\Psi\rangle_0$$

$$= e^{-i \varepsilon_n (t-t_0)} \langle n \vert\Psi\rangle_0$$

$$\leadsto \vert\Psi(t)\rangle = \sum_n \vert n\rangle \underline{\langle n ... ...n\rangle \underline{e^{-i \varepsilon_n (t-t_0)} \langle n \vert\Psi\rangle_0},$$

where the underlined terms are the expansion coefficients of $\vert\Psi(t)\rangle$ in the basis $\{\vert n\rangle \}$.