




Next: Time-evolution with time-independent
Up: Time-Dependent Fields
Previous: Time-Dependent Fields
Contents
Index
The basis equation is the Schrödinger equation. For a given (time-dependent) Hamiltonian
 , the time evolution of a Dirac ket is
, the time evolution of a Dirac ket is
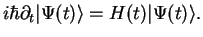 |
|
|
(1.1) |
There are usually two steps in solving a given physical problem
- find
 for the problem at hand.
for the problem at hand.
- solve the corresponding Schrödinger equation.
Depending on the problem, one often has one of the following cases:
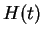 |
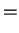 |
 time-independent Hamiltonian time-independent Hamiltonian |
(1.2) |
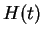 |
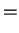 |
 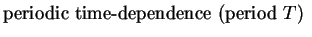 |
(1.3) |
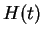 |
|
arbitrary time-dependence in Hamiltonian |
(1.4) |
The second case occurs, e.g., in the interaction of atoms with monochromatic electric fields like
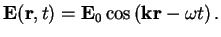 |
|
|
(1.5) |
An explicit time-dependence in the Hamiltonian usually represents classical fields or parameters that can be controlled from the outside and which are not quantum variables.
With respect to the interaction between atoms or molecules and light, there are two groups of problems one has to sort out:
- find the correct Hamiltonian
 (in fact not so easy).
(in fact not so easy).
- find appropriate techniques to solve the Schrödinger equation (at least in principle one knows how to do that).
Subsections





Next: Time-evolution with time-independent
Up: Time-Dependent Fields
Previous: Time-Dependent Fields
Contents
Index
Tobias Brandes
2005-04-26