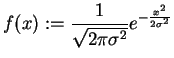Next: * Wave packet (20
Up: Fourier Transforms and the
Previous: Math: Gauß Integral 2
Contents
The Gauss function
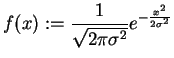 |
|
|
(2) |
is a convenient example to discuss properties of the Fourier transform.
Show that it can be decomposed into plane waves by
Draw 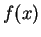 and
and
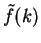 for different values of
for different values of 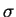 and discuss their relation.
and discuss their relation.
Tobias Brandes
2004-02-04