



Next: Position and Momentum in
Up: Fourier Transforms and the
Previous: Math: Fourier Transform of
Contents
We assume that a particle with energy 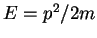 can be described by a function that is a superposition of
plane waves,
can be described by a function that is a superposition of
plane waves,
Use
to calculate the wave packet
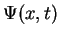 . Here,
. Here, 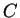 is a constant. Show that
To simplify your calculation, you
can set
is a constant. Show that
To simplify your calculation, you
can set
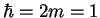 during your calculation and re-install it in the result. Why does this
`trick' work? Discuss
during your calculation and re-install it in the result. Why does this
`trick' work? Discuss 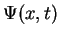 as a function of time.
as a function of time.
Tobias Brandes
2004-02-04
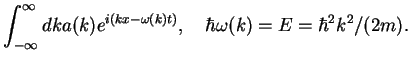
![$\displaystyle \Psi(x,t)= \frac{C}{\sqrt{1+i(\hbar t/m\sigma^2)}}
\exp{\left(-\frac{x^2}{2\sigma^2[1+i(\hbar t/m\sigma^2)]}\right)}.
$](img41.png)