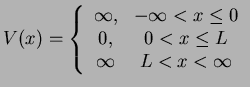Next: Energies and Eigenstates II
Up: The Infinite Potential Well
Previous: The Infinite Potential Well
Contents
Consider the motion of a particle of mass 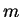 within the interval
within the interval
![$ [x_1,x_2]=[0,L], L>0$](img57.png) between the infinitely high walls of the potential
between the infinitely high walls of the potential
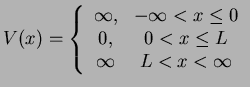 |
(7) |
Show that the normalized energy eigenstate wave functions and energies are
Tobias Brandes
2004-02-04