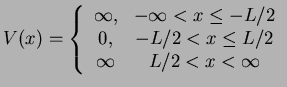Energies and Eigenstates II (10-20 min)

Consider the motion of a particle of mass 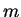$m$ within the infinitely high potential well

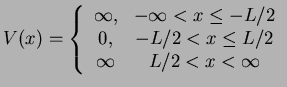$$V(x)=\left\{ \begin{array}{cc} \infty, & -\infty<x\le -L/2 \\ 0, & -L/2<x\le L/2 \\ \infty & L/2<x< \infty \end{array} \right.$$ (9)

Determine the eigenfunctions 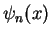$\psi_n(x)$ and energy eigenvalues 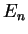$E_n$ explicitly. What are the symmetry properties of the eigenfunctions? Can you recover them from the solutions of the infinite well on the interval $[0,L]$ (see above and lecture notes)?