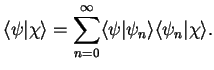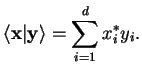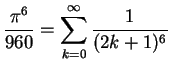Next: Operators and Measurements in
Up: Axioms of Quantum Mechanics
Previous: * Expansion into eigenmodes
Contents
a) Use the bra and ket notation to show that for an orthonormal basis
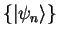 and
two Hilbert space vectors
and
two Hilbert space vectors
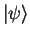 and
and
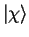 , one has
, one has
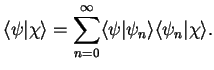 |
|
|
(28) |
b) Show that in the case of vectors 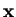 ,
,
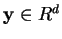 , this reduces to the
standard formula for the scalar product in
, this reduces to the
standard formula for the scalar product in 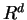 ,
,
c) Use Eq.(3.28) and
Eq.(3.27) to prove
Tobias Brandes
2004-02-04