



Next: Wave Mechanics
Up: Position and Momentum in
Previous: Example: Wave packet
Contents
Position 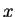 and momentum
and momentum 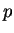 are operators in quantum mechanics.
Acting on wave functions, the operator product
are operators in quantum mechanics.
Acting on wave functions, the operator product 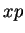 has the property
has the property
The result depends on the order of 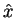 and
and 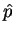 : both operators do not commute.
One has
: both operators do not commute.
One has
Comparing both sides, we have the commutation relation
Here, we have defined the commutator
![$ [A,B]:=AB-BA$](img301.png) of two operators
of two operators 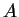 and
and 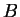 .
Generalized to three dimensions with the three components
.
Generalized to three dimensions with the three components 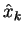 of
of
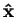 and
and
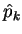 of
of
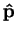 ,
, 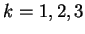 ,
one has the canonical commutation relations
,
one has the canonical commutation relations




Next: Wave Mechanics
Up: Position and Momentum in
Previous: Example: Wave packet
Contents
Tobias Brandes
2004-02-04