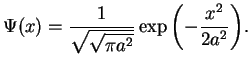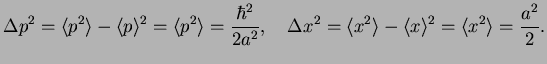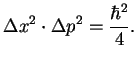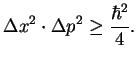Next: The commutator
Up: Position and Momentum in
Previous: Expectation values in quantum
Contents
We consider the wave function (wave packet, see above)
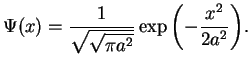 |
|
|
(70) |
1. We calculate
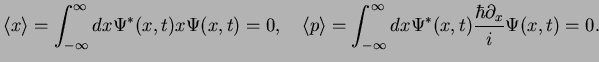 |
|
|
(71) |
2. We calculate (see problem sheet 1)
By this we obtain for the mean square deviations of the position 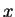 and the momentum
and the momentum 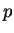 ,
The product of the two is just
The particular case of our wave packet fulfills the
Heisenberg uncertainty relation
,
The product of the two is just
The particular case of our wave packet fulfills the
Heisenberg uncertainty relation
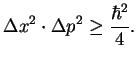 |
|
|
(73) |
with the 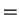 -sign. We will later prove that there are
Heisenberg uncertainty relations for arbitrary pairs of operators and not only for
-sign. We will later prove that there are
Heisenberg uncertainty relations for arbitrary pairs of operators and not only for
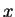 and
and 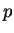 .
.




Next: The commutator
Up: Position and Momentum in
Previous: Expectation values in quantum
Contents
Tobias Brandes
2004-02-04