



Next: Example: Wave packet
Up: Position and Momentum in
Previous: Position and Momentum in
Contents
We had seen that the square of the wave function,
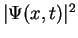 ,
describing a particle in a potential
,
describing a particle in a potential 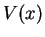 , is a probability density to find the particle
at
, is a probability density to find the particle
at 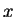 at time
at time 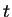 . The result
of a single measurement of
. The result
of a single measurement of 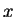 can only be predicted to have a certain probability, but
if many measurements of the position
can only be predicted to have a certain probability, but
if many measurements of the position 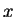 under identical conditions
are repeated, the average value (expectation value) of
under identical conditions
are repeated, the average value (expectation value) of 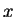 is
is
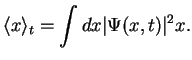 |
|
|
(58) |
We have again adopted a one-dimensional version for simplicity, in three dimensions the expectation value is completely
analogous,
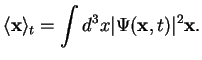 |
|
|
(59) |
Note that the expectation value is now
a three-dimensional vector which is a function of time 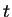 . We have indicated the time-dependence
by the notation
. We have indicated the time-dependence
by the notation
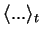 .
.
Next, we would like to know the expectation value of the momentum 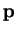 of the particle.
To determine
of the particle.
To determine 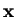 and
and 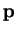 for a given massive object (like a planet
revolving around the sun) at time
for a given massive object (like a planet
revolving around the sun) at time 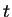 is one of the aims of classical mechanics.
In quantum mechanics, we only have the probability density
is one of the aims of classical mechanics.
In quantum mechanics, we only have the probability density
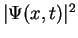 , but we can calculate
expectation values: We define the expectation value for the momentum
, but we can calculate
expectation values: We define the expectation value for the momentum 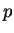 (one-dimensional version) as
(one-dimensional version) as
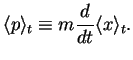 |
|
|
(60) |
This seems plausible because in classical mechanics
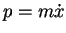 . Later we will see that
an equivalent definition is also possible, using the de Broglie relation
. Later we will see that
an equivalent definition is also possible, using the de Broglie relation 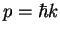 .
We write
.
We write
Now, we re-call the definition of the current-density and the continuity equation,
Eq.(1.39),
We therefore find
We compare
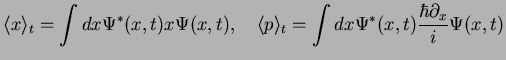 |
|
|
(63) |
and recognize that
the position 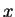 corresponds to the (somewhat trivial) operator `multiplication with
corresponds to the (somewhat trivial) operator `multiplication with 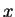 '.
On the other hand, the momentum corresponds to the completely non-trivial operator
'.
On the other hand, the momentum corresponds to the completely non-trivial operator
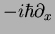 .
A similar calculation leads to
.
A similar calculation leads to
![$\displaystyle \langle x^2 \rangle_t =\int dx \Psi^*({x},t) x^2 \Psi({x},t),\qua...
...t =\int dx \Psi^*({x},t) \left[\frac{\hbar \partial_x}{i}\right]^2 \Psi({x},t).$](img265.png) |
|
|
(64) |
Again, the above can easily be generalized to three dimensions when
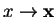 and
and
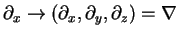 (gradient or Nabla-operator).
(gradient or Nabla-operator).
Axiom 2: Expectation values of functions
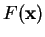 of the position or
of the position or
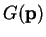 of the momentum for a quantum mechanical system described by a wave function
of the momentum for a quantum mechanical system described by a wave function
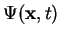 are calculated
as
are calculated
as
The position 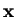 corresponds to the operator `multiplication with
corresponds to the operator `multiplication with 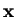 ', the
momentum
', the
momentum 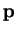 to the operator
to the operator
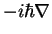 , applied to the wave function as in
(1.63),(1.64),(1.65).
, applied to the wave function as in
(1.63),(1.64),(1.65).
This correspondence in particular holds for the total energy, which in classical mechanics
for a conservative system (energy is conserved) is given by a Hamilton function
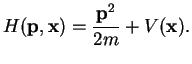 |
|
|
(66) |
The correspondence principle from axiom 2 tells us that this Hamilton function in quantum mechanics
has to be replaced by a Hamilton operator (Hamiltonian) 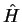
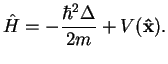 |
|
|
(67) |
Here, we have used the definition of the Laplace operator
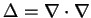 . In Cartesian
coordinates, it is
. In Cartesian
coordinates, it is
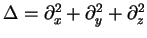 .
The Hamilton operator represents the total energy of the particle with mass
.
The Hamilton operator represents the total energy of the particle with mass 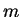 in the potential
in the potential
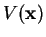 .
We have introduced the hat as a notation for operators, but often the hat is omitted for simplicity.
We make the important observation that
.
We have introduced the hat as a notation for operators, but often the hat is omitted for simplicity.
We make the important observation that 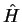 is exactly the expression that appears on the right hand
side of
the Schrödinger equation (1.21). This means we can write the Schrödinger equation as
is exactly the expression that appears on the right hand
side of
the Schrödinger equation (1.21). This means we can write the Schrödinger equation as
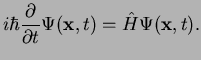 |
|
|
(68) |
This is the most general form of the Schrödinger equation in quantum mechanics. The replacement of
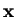 and
and 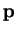 in quantum mechanics is
in quantum mechanics is
Axiom 3: The position 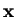 and momentum
and momentum 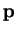 are
operators acting on wave functions,
are
operators acting on wave functions,
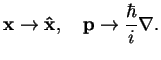 |
|
|
(69) |




Next: Example: Wave packet
Up: Position and Momentum in
Previous: Position and Momentum in
Contents
Tobias Brandes
2004-02-04
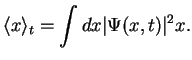
![]() of the particle.
To determine
of the particle.
To determine ![]() and
and ![]() for a given massive object (like a planet
revolving around the sun) at time
for a given massive object (like a planet
revolving around the sun) at time ![]() is one of the aims of classical mechanics.
In quantum mechanics, we only have the probability density
is one of the aims of classical mechanics.
In quantum mechanics, we only have the probability density
![]() , but we can calculate
expectation values: We define the expectation value for the momentum
, but we can calculate
expectation values: We define the expectation value for the momentum ![]() (one-dimensional version) as
(one-dimensional version) as
![$\displaystyle \fbox{$ \begin{array}{rcl} \displaystyle
& &\frac{\partial}{\part...
...si(x,t)
- \Psi(x,t)\frac{\partial}{\partial x}\Psi^*(x,t)\right].
\end{array}$}$](img179.png)
![$\displaystyle {\mbox{\rm [partial integration]}} = m \int dx j(x,t) ={\mbox{\rm [definition of j]}}$](img259.png)
![$\displaystyle -\frac{i\hbar}{2} \int dx
[\Psi^*({x},t)\partial_x \Psi({x},t)-\Psi({x},t)\partial_x \Psi^*({x},t)]
={\mbox{\rm [partial integration]}}$](img260.png)
![$\displaystyle -\frac{i\hbar}{2} \int dx
[\Psi^*({x},t)\partial_x \Psi({x},t)+\partial_x\Psi({x},t) \Psi^*({x},t)]$](img261.png)
![$\displaystyle \int dx [\Psi^*({x},t)\frac{\hbar \partial_x}{i} \Psi({x},t)].$](img262.png)
![]() of the position or
of the position or
![]() of the momentum for a quantum mechanical system described by a wave function
of the momentum for a quantum mechanical system described by a wave function
![]() are calculated
as
are calculated
as
![]() and momentum
and momentum ![]() are
operators acting on wave functions,
are
operators acting on wave functions,