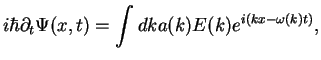Next: Interpretation of the Wave
Up: Waves, particles, and wave
Previous: Introduction
Contents
Let us come back to de Broglie's idea to describe a particle as a wave or better as a superposition
of waves.
We assume that a particle with energy 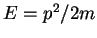 can be described by a function that is a superposition of
plane waves,
can be described by a function that is a superposition of
plane waves,
We have used the relation between momentum and wave vector, 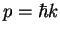 , and
the relation between energy and angular frequency,
, and
the relation between energy and angular frequency,
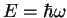 . As with waves, the
angular frequency
. As with waves, the
angular frequency 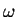 in general depends on the wave length and therefore
in general depends on the wave length and therefore
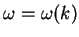 .
For simplicity, we adopted a one-dimensional version.
Note that the time evolution of a single plane wave
.
For simplicity, we adopted a one-dimensional version.
Note that the time evolution of a single plane wave
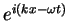 goes with the minus sign.
We would like to know the time evolution of the function
goes with the minus sign.
We would like to know the time evolution of the function 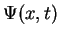 , i.e. to find its equation of motion.
Equations of motion often represent fundamental laws in physics, like Newton's
, i.e. to find its equation of motion.
Equations of motion often represent fundamental laws in physics, like Newton's 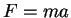 , which is a second
order differential equation
, which is a second
order differential equation
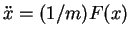 . We therefore differentiate (1.17)
with respect to time (we write
. We therefore differentiate (1.17)
with respect to time (we write
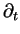 for
for
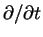 etc.
etc.
So far we have only considered a particle that only has kinetic energy
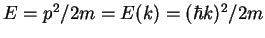 .
In general, a particle can have both kinetic energy and potential energy
.
In general, a particle can have both kinetic energy and potential energy 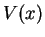 .
.
Example: A harmonic oscillator with
angular frequency 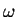 and mass
and mass 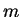 in one dimension has the potential energy
in one dimension has the potential energy
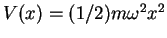 .
.
We now postulate that the above equation for a free particle (zero potential energy),
has to be generalized by replacing 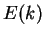 with the total energy
with the total energy 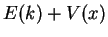 for a particle
in a non-zero potential. Then, the equation of motion becomes
for a particle
in a non-zero potential. Then, the equation of motion becomes
The equation
![$\displaystyle i\hbar\frac{\partial}{\partial t} \Psi(x,t)
=\left[-\frac{\hbar^2\partial_x^2}{2m} + V(x) \right]\Psi(x,t)$](img117.png) |
|
|
(20) |
is called Schrödinger equation and is one of the most important equations of physics at all.
We only have given the one-dimensional version of it so far, the generalization to two or three dimensions
is not difficult: the variables 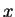 and
and  become vectors
become vectors 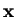 and
and 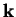 .
Instead of the differential operator
.
Instead of the differential operator
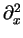 , one has
, one has
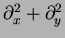 in two or
in two or
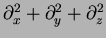 in three
dimensions. This is nothing else but the Laplace operator
in three
dimensions. This is nothing else but the Laplace operator
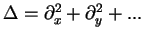 .
The Schrödinger equation reads
.
The Schrödinger equation reads
![$\displaystyle i\hbar\frac{\partial}{\partial t} \Psi({\bf x},t)
=\left[-\frac{\hbar^2\Delta}{2m} + V({\bf x}) \right]\Psi({\bf x},t).$](img125.png) |
|
|
(21) |




Next: Interpretation of the Wave
Up: Waves, particles, and wave
Previous: Introduction
Contents
Tobias Brandes
2004-02-04
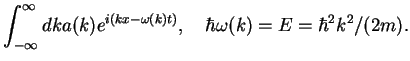
![]() and mass
and mass ![]() in one dimension has the potential energy
in one dimension has the potential energy
![]() .
.