



Next: The wave packet
Up: Waves, particles, and wave
Previous: Waves, particles, and wave
Contents
After our relatively detailed historic introduction above,
we only shortly touch the important other findings that lead to
quantum mechanics. The first is the photoelectric effect, discovered by Hertz in 1887 in tin plates that got
positively charged when irradiated with UV light.
Electrons are emitted from a metal surface only if the
frequency is above a certain limit.
Also, experiments by Philipp Lenard ![[*]](file:/usr/share/latex2html/icons/footnote.png) showed that the kinetic energy
showed that the kinetic energy 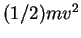 is independent of the intensity of the radiation.
Einstein explained this effect in 1905
by introducing discrete quanta of light, i.e. photons, with energy
is independent of the intensity of the radiation.
Einstein explained this effect in 1905
by introducing discrete quanta of light, i.e. photons, with energy
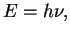 |
|
|
(11) |
which are absorbed in order to kick an electron out of the metal.
Energy conservation requires
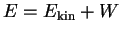 , where
, where 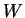 the `work function', i.e. the energy to get the electrons out of the metal, and
the `work function', i.e. the energy to get the electrons out of the metal, and
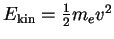 is the additional kinetic energy of the electron (mass
is the additional kinetic energy of the electron (mass 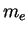 ) when it has
a finite velocity
) when it has
a finite velocity 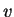 .
On the other hand, the general expression for the total energy of a particle is
.
On the other hand, the general expression for the total energy of a particle is
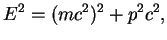 |
|
|
(12) |
and for photons that move with the velocity of light 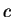 the mass (rest mass)
the mass (rest mass) 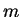 must be zero. This yields
must be zero. This yields
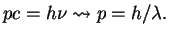 |
|
|
(13) |
Introducing the wave vector 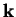 with
with
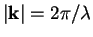 , pointing in the same
direction as
, pointing in the same
direction as 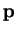 , this
establishes the relation between momentum and wave vector,
, this
establishes the relation between momentum and wave vector,
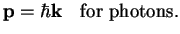 |
|
|
(14) |
In particular, the photoelectric effect showed that light has a particle aspect. On the other hand, it was known that
interference etc. were consequences of the wave properties of light.
In 1923, this particle-wave duality was extended to matter, i.e. massive objects, by de Broglie.
Wave properties of matter had already been discussed in the 19th century by Hamilton. It was known that
geometrical optics could be derived from the wave theory of light (Eikonal equation). In a similar way, there
was an Eikonal equation in a branch of theoretical mechanics called Hamilton-Jacobi theory.
By this one could speculate that classical mechanics had to be a limiting case of some
more complete theory (quantum mechanics), in the same spirit as geometrical optics is the limiting case
of wave theory.
A
non-relativistic, freely moving particle of mass 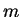 and momentum
and momentum 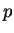 has a kinetic energy
has a kinetic energy 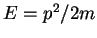 . If the
particle-wave duality can be extended from photons to massive objects, this particle also can be considered
as a wave, and one could postulate the same relation between momentum and wave vector as for photons,
. If the
particle-wave duality can be extended from photons to massive objects, this particle also can be considered
as a wave, and one could postulate the same relation between momentum and wave vector as for photons,
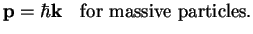 |
|
|
(15) |
Further experimental hints stem from experiments where electrons are scattered at crystal surfaces
and behave like waves (Davisson, Germer).
The de-Broglie relation means that a particle can be described as a wave with wave vector 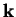 and
angular frequency
and
angular frequency 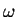 . The simplest form of such a wave is a plane wave
. The simplest form of such a wave is a plane wave
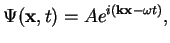 |
|
|
(16) |
but how should this quantity (which is a complex and not a real number)describe a particle? One could
form real superpositions into 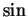 and
and 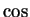 , but even then this `particle' would be extended from
minus to plus infinity which seems absolutely awkward. Intuition tells one that a particle should be
localized in space; at any fixed time
, but even then this `particle' would be extended from
minus to plus infinity which seems absolutely awkward. Intuition tells one that a particle should be
localized in space; at any fixed time 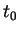 it should be at some point
it should be at some point 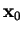 somewhere in space.
Still, going ahead with the wave concept of matter, one can form superpositions of plane waves.
somewhere in space.
Still, going ahead with the wave concept of matter, one can form superpositions of plane waves.




Next: The wave packet
Up: Waves, particles, and wave
Previous: Waves, particles, and wave
Contents
Tobias Brandes
2004-02-04
![]() and momentum
and momentum ![]() has a kinetic energy
has a kinetic energy ![]() . If the
particle-wave duality can be extended from photons to massive objects, this particle also can be considered
as a wave, and one could postulate the same relation between momentum and wave vector as for photons,
. If the
particle-wave duality can be extended from photons to massive objects, this particle also can be considered
as a wave, and one could postulate the same relation between momentum and wave vector as for photons,
![]() and
angular frequency
and
angular frequency ![]() . The simplest form of such a wave is a plane wave
. The simplest form of such a wave is a plane wave