



Next: Fourier Transforms and the
Up: Interpretation of the Wave
Previous: Expectation value (mean value),
Contents
We generate one equation by
multiplying the Schrödinger equation with
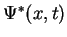 , where
, where 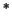 means conjugate complex.
We generate another equation by
multiplying the (Schrödinger equation)
means conjugate complex.
We generate another equation by
multiplying the (Schrödinger equation)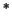 with
with
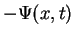 and add both equations. The result is
and add both equations. The result is
This can be written in the form of a continuity equation:
![$\displaystyle \fbox{$ \begin{array}{rcl} \displaystyle
& &\frac{\partial}{\part...
...si(x,t)
- \Psi(x,t)\frac{\partial}{\partial x}\Psi^*(x,t)\right].
\end{array}$}$](img179.png) |
|
|
(39) |
You should check that beside the probability density 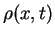 also the
probability current density
also the
probability current density 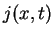 both are real quantities.
Eq. (1.39) in fact is the one-dimensional version of a continuity equation
both are real quantities.
Eq. (1.39) in fact is the one-dimensional version of a continuity equation
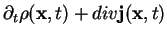 |
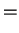 |
0 |
(40) |
that appears in different areas of physics such as fluid dynamics or wave theory.
We note that for simplicity up to here we have only dealt with the one-dimensional version of
the Schrödinger equation which yields the one-dimensional version of the
continuity equation.
We integrate Eq. (1.39) from 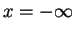 to
to 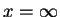 and assume that
and assume that
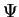 vanishes at infinity which is plausible:
if
vanishes at infinity which is plausible:
if 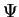 is related to a probability, this probability
should be zero at points of space that are inaccessible to the particles, i.e. at
infinity.
We obtain
is related to a probability, this probability
should be zero at points of space that are inaccessible to the particles, i.e. at
infinity.
We obtain
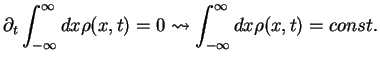 |
|
|
(41) |
The statistical interpretation of 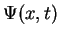 is one of the central axioms of quantum mechanics.
is one of the central axioms of quantum mechanics.




Next: Fourier Transforms and the
Up: Interpretation of the Wave
Previous: Expectation value (mean value),
Contents
Tobias Brandes
2004-02-04
![$\displaystyle -\frac{\hbar^2}{2m}\left[ \Psi^*\partial_x^2\Psi- \Psi\partial_x^2\Psi^*\right]$](img176.png)
![$\displaystyle -\frac{\hbar^2}{2m}\partial_x \left[ \Psi^*\partial_x\Psi- \Psi\partial_x\Psi^*\right].$](img178.png)