The Hilbert space ${\cal H}$ of wave functions

We have seen that the wave functions with fixed energy $E$ of a particle of mass $m$ in an infinitely high potential well of width $L$ are given by

$$\psi_n(x) = \sqrt{\frac{2}{L}}\sin \left(\frac{n\pi x}{L}\right ),\quad E= E_n= \frac{n^2 \hbar^2 \pi^2}{2mL^2},\quad n=1,2,3,...$$ (100)

1. We have omitted the arbitrary phase factor $e^{i\varphi}$ here as discussed above.

2. The index $n$ is called quantum number, it labels the possible solutions of the stationary Schrödinger equation

$$\hat{H}\psi_n(x)=E_n\psi_n(x).$$ (101)

As in linear algebra, the $E_n$ are called eigenvalues (eigenvalues of the energy) and the $\psi_n(x)$ are called eigenvectors (eigenfunctions) of the Hamiltonian ${\hat{H}}$.

3. We only have positive integers $n$: negative integers $-\vert n\vert$ would lead to solutions $\psi_{-\vert n\vert}(x)=-\psi_n(x)$ which are just the negative of the wave functions with positive $n$. They describe the same state of the particle which is unique up to a phase $e^{i\varphi}$ (for example $e^{i\varphi}=-1$) anyway. $\psi_{-\vert n\vert}(x)$ is linear dependent on $\psi_{n}(x)$.

4. The eigenvectors of $\hat{H}$, i.e. the functions $\psi_n(x)$, form the basis of a linear vector space ${\cal H}$ of functions $f(x)$ defined on the interval $[0,L]$ with $f(0)=f(L)=0$. The $\psi_n(x)$ form an orthonormal basis:

$$\int_0^Ldx \vert\psi_n(x)\vert^2=1,\quad \int_0^Ldx \psi_n^*(x)\psi_m(x)=\delta_{nm}.$$ (102)

(We can omit the $*$ here because the $\psi_n$ are real). Note that the orthonormal basis is of infinite dimension because there are infinitely many $n$. The infinite dimension of the vector space (function space) ${\cal H}$ is the main difference to ordinary, finite dimensional vector spaces like the $R^3$.

5. Any wave function $\psi(x) \in {\cal H}$ (like any arbitrary vector in, e.g., the vector space $R^3$) can be expanded into a linear combination of basis `vectors', i.e. eigenfunctions $\psi_n(x)$:

$$\psi(x)=\sum_{n=1}^{\infty}c_n\psi_n(x),\quad c_n=\int_0^Ldx \psi(x)\psi_n(x).$$ (103)

A vector space with these properties is called a Hilbert space. The Hilbert space is the central mathematical object of quantum theory.

Example	vectors and matrices	Particle in Quantum Well
vector	${\bf x}$	wave function $\psi(x)$
space	vector space	Hilbert space
linear operator	matrix 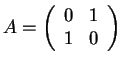$A=\left( \begin{array}{ll} 0&1\\ 1&0 \end{array}\right)$	Hamiltonian $H_{\rm well}$
eigenvalue problem	$A{\bf x} = \lambda {\bf x}$	$H_{\rm well} \psi_n = E_n \psi_n$
eigenvalue	$\lambda_1 = 1,\lambda_2=-1$	$E_n =\frac{n^2\pi^2\hbar^2}{2mL},n=1,2,3...$
eigenvector	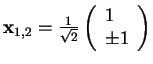${\bf x}_{1,2}=\frac{1}{\sqrt{2}}\left( \begin{array}{l} 1\\ \pm 1 \end{array}\right)$	wave function $\psi_n(x)=\sqrt{\frac{2}{L}}\sin \left(\frac{n\pi x}{L}\right )$
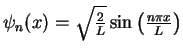scalar product	$\langle {\bf x} \vert {\bf y} \rangle \equiv \sum_{n=1}^2 x_n^*y_n$	$\langle \psi \vert \phi \rangle \equiv \int_0^Ldx \psi^*(x)\phi(x)$
orthogonal basis	$\langle {\bf e}_n \vert {\bf e}_m \rangle=\delta_{nm}$	$\langle \psi_n \vert \psi_m \rangle =\delta_{nm}$
dimension	$2$	$\infty$
completeness	${\bf x}=\sum_{n=1}^2\langle {\bf e}_n\vert{\bf x} \rangle{\bf e}_n$	$\psi =\sum_{n=1}^{\infty}\langle \psi_n \vert \psi \rangle \psi_n$
vector components	${\bf x} = (\langle {\bf e}_1\vert{\bf x} \rangle,\langle {\bf e}_2\vert{\bf x} \rangle)$	$\psi = (\langle \psi_1 \vert \psi \rangle, \langle \psi_2 \vert \psi \rangle,...)$

We will explain this table in greater detail in the next chapter where we turn to the foundations of quantum mechanics.