



Next: The Hilbert space of
Up: The Infinite Potential Well
Previous: The Infinite Potential Well
Contents
We first study the case where the motion of the particle is restricted
within the interval
![$ [x_1,x_2]=[0,L], L>0$](img377.png) between the infinitely high walls of the potential
between the infinitely high walls of the potential
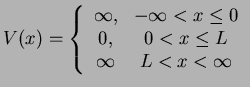 |
(94) |
Outside the interval ![$ [0,L]$](img379.png) the particle can not exist and its wave function
must be zero, i.e.
the particle can not exist and its wave function
must be zero, i.e.
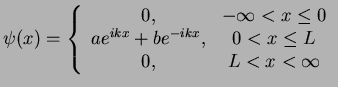 |
(95) |
1. We demand that the wave function vanishes
at 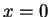 and
and 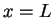 so that it is continuous a these points.
Clearly, this makes physically sense because at
so that it is continuous a these points.
Clearly, this makes physically sense because at 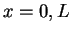 the potential is
infinitely high and the probability density
the potential is
infinitely high and the probability density
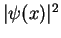 to find the particle there
should be zero. We obtain
to find the particle there
should be zero. We obtain
The first condition tells us that the wave function must be a sine-function. The second
condition is more interesting: it sets a condition for the possible values 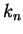 that
that  can have,
can have,
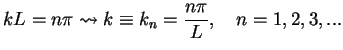 |
|
|
(97) |
The second boundary condition at 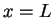 restricts the possible values of the energy
restricts the possible values of the energy  ,
because
,
because
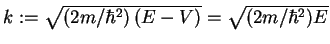 . Therefore,
the energy can only acquire values
. Therefore,
the energy can only acquire values
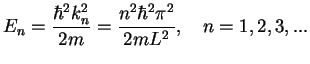 |
|
|
(98) |
This is the first case where we encounter a quantisation of energy. The reason for the
quantization here is obvious: the wave functions 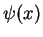 have to `fit' into the
well, similar to classical waves in a resonator which only allows waves with certain wave lengths .
The allowed wave vectors
have to `fit' into the
well, similar to classical waves in a resonator which only allows waves with certain wave lengths .
The allowed wave vectors 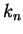 then are related to the energy by the de Broglie relation
then are related to the energy by the de Broglie relation
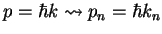 , and the energy within the well is just the kinetic
energy
, and the energy within the well is just the kinetic
energy 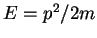 (since the potential is zero there) whence (2.21) follows.
(since the potential is zero there) whence (2.21) follows.
2. The potential well gives only rise to discrete values of the energy.
One says that the spectrum of energies is discrete. If we did not have the confinement potential, the wave
functions would just be plane waves
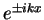 with arbitrary values
with arbitrary values  and therefore
arbitrary, continues values for the energies
and therefore
arbitrary, continues values for the energies
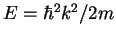 . In such a case the
the spectrum is called a continuous spectrum.
. In such a case the
the spectrum is called a continuous spectrum.
3. In order to interpret the absolute square wave of the wave functions
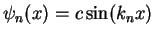 as a probability density, we have to demand
as a probability density, we have to demand
where
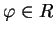 is a (real) phase factor. This normalization condition
determines the wave functions
is a (real) phase factor. This normalization condition
determines the wave functions 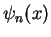 uniquely only up to a phase factor:
if
uniquely only up to a phase factor:
if 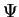 is a normalized solution of the Schrödinger equation, so is
is a normalized solution of the Schrödinger equation, so is
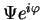 , i.e. the same wave function multiplied with a constant overall
phase factor. Usually, we do not distinguish between such wave functions since
they describe the same state of the particle, and one says that the state
is only determined `up to a phase' which is irrelevant when calculating, for example,
the probability density
, i.e. the same wave function multiplied with a constant overall
phase factor. Usually, we do not distinguish between such wave functions since
they describe the same state of the particle, and one says that the state
is only determined `up to a phase' which is irrelevant when calculating, for example,
the probability density 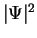 or expectation values.
or expectation values.
This is different, however, for superpositions of two different wave functions, where
the relative phase difference is important and leads, for example, to interference.




Next: The Hilbert space of
Up: The Infinite Potential Well
Previous: The Infinite Potential Well
Contents
Tobias Brandes
2004-02-04
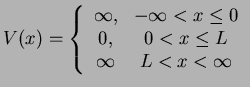
![]() with arbitrary values
with arbitrary values ![]() and therefore
arbitrary, continues values for the energies
and therefore
arbitrary, continues values for the energies
![]() . In such a case the
the spectrum is called a continuous spectrum.
. In such a case the
the spectrum is called a continuous spectrum.
![]() as a probability density, we have to demand
as a probability density, we have to demand