



Next: The parity
Up: The Potential Well
Previous: The Potential Well
Contents
Our second one-dimensional problem is
the motion of a particle in a potential well of finite depth 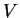 and width
and width 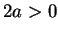 , i.e. a potential
, i.e. a potential
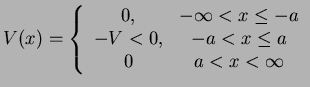 |
(104) |
According to our
general equation,
the wave functions for energies
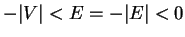 must have the form
must have the form
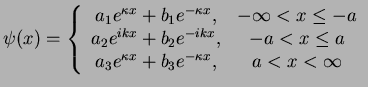 |
(105) |
where
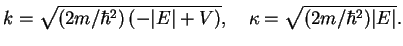 |
|
|
(106) |
The wave function has to vanish for
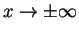 which can only be fulfilled if
which can only be fulfilled if 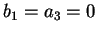 .
.
Tobias Brandes
2004-02-04