



Next: Even and odd solutions
Up: The Potential Well
Previous: Wave functions and energy
Contents
For symmetric potentials
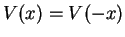 , the Schrödinger equation has an important property:
If
, the Schrödinger equation has an important property:
If 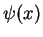 is a solution of
is a solution of
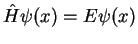 , then also
, then also 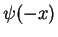 is a solution
with the same
is a solution
with the same  , i.e.
, i.e.
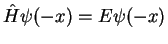 (replace
(replace 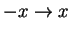 and note that
and note that
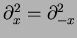 . Since
. Since 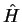 is linear, also linear combinations
of solutions with the same eigenvalue
is linear, also linear combinations
of solutions with the same eigenvalue  are solutions with eigenvalue
are solutions with eigenvalue  , in particular
the symmetric (even) and anti symmetric (odd) linear combinations
, in particular
the symmetric (even) and anti symmetric (odd) linear combinations
![$\displaystyle \psi_e(x):=\frac{1}{\sqrt{2}}[\psi(x)+\psi(-x)],\quad
\psi_o(x):=\frac{1}{\sqrt{2}}[\psi(x)-\psi(-x)].$](img455.png) |
|
|
(107) |
These are the solutions with even (e) and odd (o) parity, respectively.
Tobias Brandes
2004-02-04
![$\displaystyle \psi_e(x):=\frac{1}{\sqrt{2}}[\psi(x)+\psi(-x)],\quad
\psi_o(x):=\frac{1}{\sqrt{2}}[\psi(x)-\psi(-x)].$](img455.png)