



Next: Scattering states in one
Up: The Potential Well
Previous: The parity
Contents
Applied to our potential well, we can classify the solutions into even and odd,
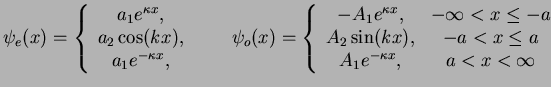 |
(108) |
The wave function 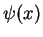 and its derivative
and its derivative 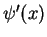 have to be
continuous at
have to be
continuous at 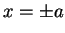 . Therefore, also the logarithmic derivative
. Therefore, also the logarithmic derivative
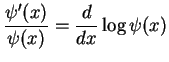 |
|
|
(109) |
has to be continuous. This is a convenient way to obtain an equation that relates  and
and 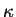 and determines the possible energy values: we calculate the logarithmic derivative for
and determines the possible energy values: we calculate the logarithmic derivative for
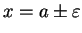 ,
,
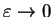 which yields
which yields
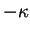 |
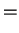 |
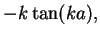 even solution even solution |
|
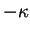 |
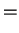 |
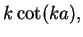 odd solution odd solution |
|
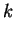 |
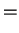 |
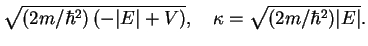 |
(110) |
These are transcendent equations for the energy  : we introduce auxiliary dimensionless variables
: we introduce auxiliary dimensionless variables
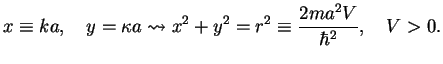 |
|
|
(111) |
The equations
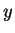 |
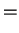 |
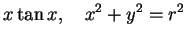 even solution even solution |
|
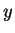 |
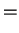 |
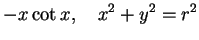 odd solution odd solution |
(112) |
describe two curves in the 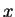 -
-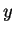 -plane, i.e. the circle
-plane, i.e. the circle
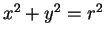 ,
with
,
with
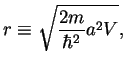 |
|
|
(113) |
and the
curve
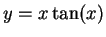 (
(
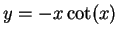 for the odd solution), whose intersections
determine a fixed number of points
for the odd solution), whose intersections
determine a fixed number of points 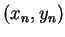 in the quadrant of positive
in the quadrant of positive
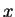 and
and 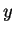 . These determine the energy eigenvalues
. These determine the energy eigenvalues 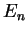 via the definition of
via the definition of
 and
and 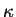 . Of course, the
. Of course, the 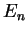 depend on the value of the parameter
depend on the value of the parameter
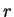 which in turn is determined by the depth of the potential well
which in turn is determined by the depth of the potential well 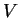 ,
its width
,
its width 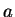 and the particle mass
and the particle mass 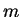 .
.
Figure:
Graphical solution of (2.35) for
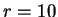 (left) and
(left) and 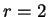 (right).
(right).
|
|
To obtain precise values for the possible energy eigenvalue 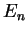 , one has to numerically solve
(2.35). A convenient method to obtain a qualitative picture, however, is
the graphical solution of the transcendent equations as shown in Fig. (2.1).
The intersections
, one has to numerically solve
(2.35). A convenient method to obtain a qualitative picture, however, is
the graphical solution of the transcendent equations as shown in Fig. (2.1).
The intersections 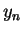 ,
, 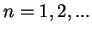 of the
of the 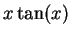 - or
- or
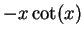 -curves with the circle
of radius
-curves with the circle
of radius 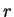 determine
determine 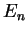 via
via
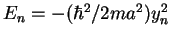 (remember that we have required
(remember that we have required 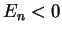 )
)
1. There are only a finite number 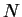 of solutions for the energies
of solutions for the energies
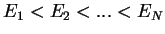 depending
on the value of the parameter
depending
on the value of the parameter 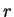 .
.
2. The wave function corresponding to the lowest eigenvalue 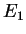 is even. Even and odd solutions
alternate when `climbing up' the ladder of possible eigenvalues
is even. Even and odd solutions
alternate when `climbing up' the ladder of possible eigenvalues 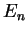 .
.




Next: Scattering states in one
Up: The Potential Well
Previous: The parity
Contents
Tobias Brandes
2004-02-04
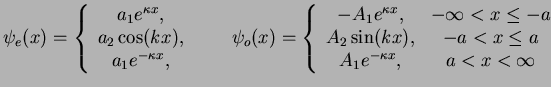
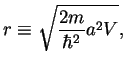
![]() , one has to numerically solve
(2.35). A convenient method to obtain a qualitative picture, however, is
the graphical solution of the transcendent equations as shown in Fig. (2.1).
The intersections
, one has to numerically solve
(2.35). A convenient method to obtain a qualitative picture, however, is
the graphical solution of the transcendent equations as shown in Fig. (2.1).
The intersections ![]() ,
, ![]() of the
of the ![]() - or
- or
![]() -curves with the circle
of radius
-curves with the circle
of radius ![]() determine
determine ![]() via
via
![]() (remember that we have required
(remember that we have required ![]() )
)
![]() of solutions for the energies
of solutions for the energies
![]() depending
on the value of the parameter
depending
on the value of the parameter ![]() .
.
![]() is even. Even and odd solutions
alternate when `climbing up' the ladder of possible eigenvalues
is even. Even and odd solutions
alternate when `climbing up' the ladder of possible eigenvalues ![]() .
.