



Next: Potential scattering
Up: Scattering states in one
Previous: Scattering states in one
Contents
The simplest case is the one where the potential 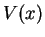 is zero throughout: the two
independent solutions of the Schrödinger
equation then are plane waves
is zero throughout: the two
independent solutions of the Schrödinger
equation then are plane waves
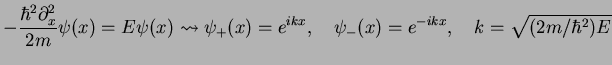 |
|
|
(114) |
with positive energy 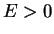 .
We denote both solutions as
.
We denote both solutions as
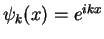 with
with  either positive or negative. They are plane waves with fixed wave vector
either positive or negative. They are plane waves with fixed wave vector
 and therefore fixed momentum
and therefore fixed momentum 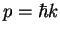 .
We can have no physically meaningful solutions with negative energy
.
We can have no physically meaningful solutions with negative energy 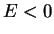 because in this case the wave function would become infinite either for
because in this case the wave function would become infinite either for
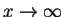 or
or
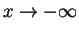 .
.
A problem arises, however, because
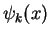 can not be
normalized over the whole
can not be
normalized over the whole 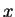 -axis according to
-axis according to
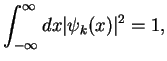 |
|
|
(115) |
because this integral is infinite: the probability density, i.e. the square
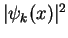 is
constant, i.e.
is
constant, i.e. 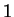 everywhere.
everywhere.
In particular, we have for the mean square deviation of the momentum and the position
There is no uncertainty in the momentum of the particle, but there is maximum uncertainty
in its position: the wave function 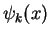 describes a particle with fixed momentum
describes a particle with fixed momentum 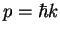 which is completely delocalized (spread) over the
which is completely delocalized (spread) over the  -axis.
-axis.
A practical solution is to consider a large, but finite interval
![$ [-L/2,L/2]$](img505.png) instead of the total
instead of the total
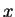 -axis, and to normalize the wave functions according to
-axis, and to normalize the wave functions according to
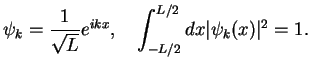 |
|
|
(117) |
Then, the boundary conditions at 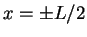 have to be specified. Again, a convenient (but not necessary
the only) choice are periodic boundary conditions: we bend the interval
have to be specified. Again, a convenient (but not necessary
the only) choice are periodic boundary conditions: we bend the interval ![$ [L/2,L/2]$](img508.png) into a ring
such that the points
into a ring
such that the points 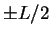 coincide. Demanding continuity of
coincide. Demanding continuity of 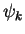 , i.e.
, i.e.
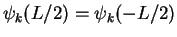 , we obtain a quantization condition for the possible
, we obtain a quantization condition for the possible  -values,
-values,
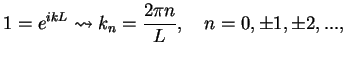 |
|
|
(118) |
i.e. a discrete set of possible  values and therewith discrete energies
values and therewith discrete energies
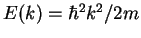 .
To each energy
.
To each energy 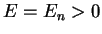 there are two linearly independent plane waves with wave vectors
there are two linearly independent plane waves with wave vectors
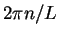 and
and 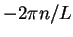 . One says the energy value
. One says the energy value 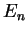 is two-fold degenerate.
If
is two-fold degenerate.
If 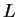 is very large, the possible values for
is very large, the possible values for  are still discrete but
subsequent
are still discrete but
subsequent  -values get very close to each other.
-values get very close to each other.




Next: Potential scattering
Up: Scattering states in one
Previous: Scattering states in one
Contents
Tobias Brandes
2004-02-04
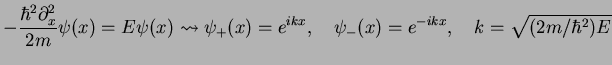
![]() can not be
normalized over the whole
can not be
normalized over the whole ![]() -axis according to
-axis according to
![]() instead of the total
instead of the total
![]() -axis, and to normalize the wave functions according to
-axis, and to normalize the wave functions according to