



Next: The Structure of Quantum
Up: Tunnel barrier potential within
Previous: Case
Contents
We wish to see how the energies and wave functions change if we lower the central barrier
from its infinite value to finite 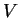 . We already expect that due to the tunnel effect, the left and
the right well, which for
. We already expect that due to the tunnel effect, the left and
the right well, which for
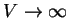 were completely separated from each other, must become
coupled now. We already know the limiting cases
were completely separated from each other, must become
coupled now. We already know the limiting cases
Introducing dimensionless variables
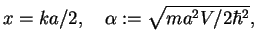 |
|
|
(160) |
we have
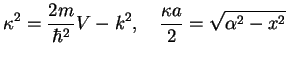 |
|
|
(161) |
and since 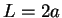 ,
,
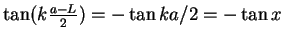 such that
the transcendent equations (2.81) become
such that
the transcendent equations (2.81) become
We expand this for large
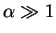 around the lowest energy solution for the case
around the lowest energy solution for the case
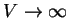 , that is around
, that is around 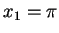 by setting
by setting 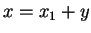 ,
, 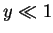 . This yields
. This yields
The corresponding wave vectors for the lowest energy solution therefore are
Since
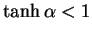 , we recognize
, we recognize 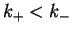 . Compared with the case
. Compared with the case
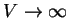 where the lowest
where the lowest  was
was
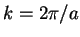 , we now have a splitting into two different
, we now have a splitting into two different  's. The lowest symmetric (even) wave function
has an energy
's. The lowest symmetric (even) wave function
has an energy
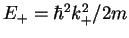 that is lower than the energy
that is lower than the energy
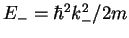 of the lowest odd wave function.
This level splitting is an important general feature appearing when
two regions in space become coupled by the tunnel effect.
of the lowest odd wave function.
This level splitting is an important general feature appearing when
two regions in space become coupled by the tunnel effect.
For very large 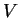 , the wave functions that belong to
, the wave functions that belong to 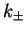 below the barrier must be very small: we see that
as
below the barrier must be very small: we see that
as
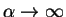 ,
,
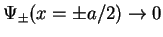 whence by continuity also the central part
of the wave function
whence by continuity also the central part
of the wave function
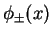 must become very small.
Then, we can approximate the wave functions for the two lowest energies
must become very small.
Then, we can approximate the wave functions for the two lowest energies 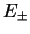 as
as
where in the definition of the left and right part wave functions
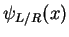 we have to use
we have to use
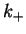 for the even and
for the even and 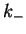 for the odd solution. In fact, for large
for the odd solution. In fact, for large 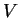 , Eq. (2.88)
tells us that the
, Eq. (2.88)
tells us that the 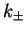 are very close to the wave vector
are very close to the wave vector 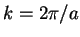 of the infinite-barrier limit,
cf. Eq. (2.83), and therefore the
of the infinite-barrier limit,
cf. Eq. (2.83), and therefore the
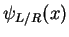 are very close to the lowest
are very close to the lowest
 -wave functions of the left and right well.
-wave functions of the left and right well.




Next: The Structure of Quantum
Up: Tunnel barrier potential within
Previous: Case
Contents
Tobias Brandes
2004-02-04
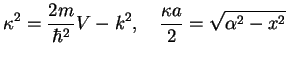
![]() , the wave functions that belong to
, the wave functions that belong to ![]() below the barrier must be very small: we see that
as
below the barrier must be very small: we see that
as
![]() ,
,
![]() whence by continuity also the central part
of the wave function
whence by continuity also the central part
of the wave function
![]() must become very small.
Then, we can approximate the wave functions for the two lowest energies
must become very small.
Then, we can approximate the wave functions for the two lowest energies ![]() as
as