



Next: Operators and The Two-Level-System
Up: Axioms of Quantum Mechanics
Previous: First Axiom: States as
Contents
Def.: An orthonormal basis
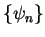 ,
,
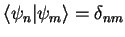 , of a Hilbert space
is called
, of a Hilbert space
is called
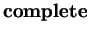 if no vector
if no vector 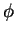 (except the zero vector) is orthogonal to all
(except the zero vector) is orthogonal to all 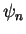 .
.
In the following, we will mostly deal with Hilbert spaces that have a complete
orthonormal basis, which guarantees the expansion of any wave function into a linear combination of
basis vectors. In most cases, the orthonormal basis consists of the eigenfunctions (eigenvectors) of the
Hamilton operator 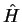 .
.
In quantum mechanics it has become common to use the symbol (`ket')
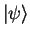 for a wave function (Hilbert space vector)
instead of
for a wave function (Hilbert space vector)
instead of 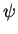 . The expansion of an arbitrary ket
. The expansion of an arbitrary ket
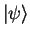 into
the orthonormal basis
into
the orthonormal basis
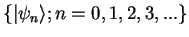 then can be written as
then can be written as
Here, the scalar product, that is the `bracket'
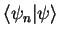 , gives rise to
define the bra vector (from `bra -cket')
, gives rise to
define the bra vector (from `bra -cket')
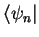 as the
state with wave function
as the
state with wave function
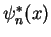 . This means that
. This means that
A very convenient way to memorize and use the completeness property
is the `insertion of the 1',
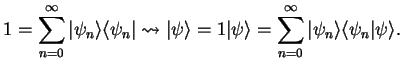 |
|
|
(179) |




Next: Operators and The Two-Level-System
Up: Axioms of Quantum Mechanics
Previous: First Axiom: States as
Contents
Tobias Brandes
2004-02-04
![]() .
.
![]() for a wave function (Hilbert space vector)
instead of
for a wave function (Hilbert space vector)
instead of ![]() . The expansion of an arbitrary ket
. The expansion of an arbitrary ket
![]() into
the orthonormal basis
into
the orthonormal basis
![]() then can be written as
then can be written as