



Next: Math: Completeness, Dirac notation
Up: Axioms of Quantum Mechanics
Previous: The Hilbert space
Contents
To conclude, we formulate our first axiom of quantum mechanics:
Axiom 1: A quantum mechanical system is described by a vector
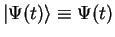 of a Hilbert space
of a Hilbert space 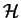 . The time evolution of
. The time evolution of 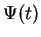 is determined by
the Schrödinger equation
is determined by
the Schrödinger equation
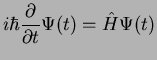 |
|
|
(174) |
The Hamilton operator 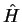 is an operator corresponding to the total
energy of the system. In the case of a single particle with mass
is an operator corresponding to the total
energy of the system. In the case of a single particle with mass 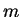 moving in the configuration space
moving in the configuration space 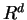 under a potential
under a potential
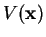 ,
the wave function
,
the wave function
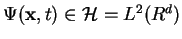 (square
integrable functions) obeys
(square
integrable functions) obeys
![$\displaystyle i\hbar\frac{\partial}{\partial t} \Psi({\bf x},t)
=\left[-\frac{\hbar^2\Delta}{2m} + V({\bf x}) \right]\Psi({\bf x},t).$](img125.png) |
|
|
(175) |
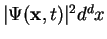 is the probability for the particle to be in the (infinitesimal small) volume
is the probability for the particle to be in the (infinitesimal small) volume 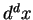 around
around
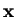 at time t.
The solutions of the stationary Schrödinger equation at fixed energy,
at time t.
The solutions of the stationary Schrödinger equation at fixed energy,
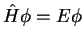 |
|
|
(176) |
are called stationary states, the possible energies  eigenenergies.
eigenenergies.
Note that the form of the Hamilton operator not necessarily has to be as in
(3.10), the Hamiltonian for a single particle defined
over the space 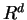 . We will later encounter, for example, Hamiltonians that describe the sites of a finite lattice
and have the form of a
. We will later encounter, for example, Hamiltonians that describe the sites of a finite lattice
and have the form of a 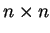 matrix.
matrix.




Next: Math: Completeness, Dirac notation
Up: Axioms of Quantum Mechanics
Previous: The Hilbert space
Contents
Tobias Brandes
2004-02-04
![]() of a Hilbert space
of a Hilbert space ![]() . The time evolution of
. The time evolution of ![]() is determined by
the Schrödinger equation
is determined by
the Schrödinger equation
![]() . We will later encounter, for example, Hamiltonians that describe the sites of a finite lattice
and have the form of a
. We will later encounter, for example, Hamiltonians that describe the sites of a finite lattice
and have the form of a ![]() matrix.
matrix.