



Next: First Axiom: States as
Up: Math: Examples of Hilbert
Previous: The -dimensional Hilbert space
Contents
This is the space of of square integrable
wave functions 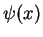 of the infinite potential well, section 2.2,
defined on the interval
of the infinite potential well, section 2.2,
defined on the interval ![$ [0,L]$](img379.png) , with
, with
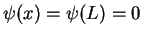 . Each function
. Each function 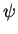 is considered as a vector,
the linear structure of a vector space comes from the fact the
is considered as a vector,
the linear structure of a vector space comes from the fact the
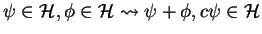 . The scalar product is given by an integral
. The scalar product is given by an integral
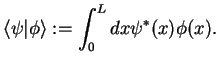 |
|
|
(170) |
You can check that this is a scalar product indeed.
The eigenvectors of the Hamiltonian 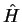 , i.e. the functions
, i.e. the functions 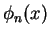 with energy
with energy 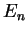 ,
,
form an orthonormal basis of 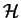
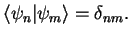 |
|
|
(172) |
Any wave function
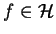 can be expanded into
a linear combination of basis vectors, i.e. eigenfunctions
can be expanded into
a linear combination of basis vectors, i.e. eigenfunctions 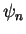 ,
,
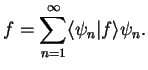 |
|
|
(173) |
We summarize the above two examples in the following table:
| example |
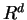 |
 |
| vector |
x |
wave function 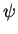 |
| scalar product |
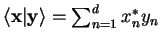 |
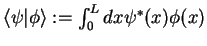 |
| orthonormal basis |
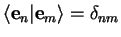 |
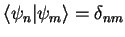 |
| completeness |
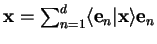 |
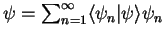 |
| components |
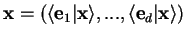 |
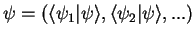 |
If you understand this table, you are already halfway in completely understanding the math
underlying quantum mechanics.




Next: First Axiom: States as
Up: Math: Examples of Hilbert
Previous: The -dimensional Hilbert space
Contents
Tobias Brandes
2004-02-04