Def.: A linear Operator ![]() acting on vectors
acting on vectors
![]() ,
,
![]() of a Hilbert space
of a Hilbert space ![]() has the property
has the property
2. The momentum operator
![]() , acting on a Hilbert space of differentiable
functions as
, acting on a Hilbert space of differentiable
functions as
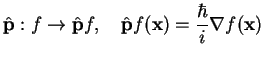
Expectation values of observables ![]() in particular should be real numbers because they represent the outcome of
an average over many measurements. We have to introduce one additional definition to clarify this concept:
in particular should be real numbers because they represent the outcome of
an average over many measurements. We have to introduce one additional definition to clarify this concept:
Def.: The adjoint operator
![]() of a linear operator
of a linear operator ![]() acting on a Hilbert space
acting on a Hilbert space
![]() is defined by
is defined by
| (191) |
Def.: A linear operator ![]() on the
Hilbert space
on the
Hilbert space ![]() is called hermitian, if the following relation holds:
is called hermitian, if the following relation holds:
| (192) |
Examples:
1. For complex two-by- two matrices
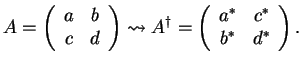
2. For complex two-by-two matrices
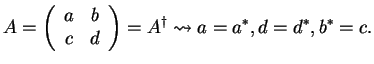
3. The momentum operator ![]() in one dimension, acting on wave functions
in one dimension, acting on wave functions
![]() that vanish at
that vanish at
![]() , is hermitian:
, is hermitian:
![$\displaystyle \langle \psi \vert \hat{p}\phi \rangle = -i\hbar \int dx \psi^*(x...
...= \int dx [-i\hbar \psi'(x)]^* \phi(x) = \langle \hat{p}\psi \vert\phi\rangle.
$](img835.png)
The expectation values of hermitian operators ![]() in any Hilbert space state vector
in any Hilbert space state vector ![]() are real indeed because
are real indeed because
| (193) |
Axiom 2b:
Physical observable quantities correspond to hermitian linear operators ![]() acting on Hilbert space vectors.
acting on Hilbert space vectors.
Furthermore, the following theorem holds:
Theorem: The eigenvalues of hermitian operators ![]() are real.
This is because
are real.
This is because
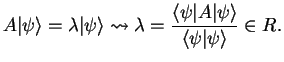 |
(194) |