These two statements belong to the Kopenhagen interpretation of quantum mechanics and are widely accepted and experimentally confirmed by now. They belong to the axioms of quantum mechanics and can be motivated as follows:
Consider a quantum mechanical system in a normalized state
![]() . We wish to perform
a measurement of a quantity (for example the energy) that is represented by a hermitian operator
. We wish to perform
a measurement of a quantity (for example the energy) that is represented by a hermitian operator ![]() (for example the Hamiltonian
(for example the Hamiltonian ![]() ).
).
CASE 1: Assume that
![]() is an eigenstate of
is an eigenstate of ![]() ,
,
![]() with eigenvalue
with eigenvalue ![]() . Repeating this measurement at many systems that are prepared in the same
way, or at the same system that is always prepared in the same state
. Repeating this measurement at many systems that are prepared in the same
way, or at the same system that is always prepared in the same state
![]() , the expectation value
of
, the expectation value
of ![]() is
is
![]() .
.
CASE 2: Assume that
![]() is not an eigenstate of
is not an eigenstate of ![]() . After a measurement with outcome
. After a measurement with outcome
![]() assume the system is in another state
assume the system is in another state
![]() . Assume immediately after the first measurement,
a second measurement with outcome
. Assume immediately after the first measurement,
a second measurement with outcome ![]() is performed. We now assume that this second measurement
should give the same outcome as the first measurement, i.e.
is performed. We now assume that this second measurement
should give the same outcome as the first measurement, i.e. ![]() . This thought experiment is repeated
many times at identically prepared systems. Always
. This thought experiment is repeated
many times at identically prepared systems. Always ![]() should come out such that the
square deviation of
should come out such that the
square deviation of ![]() for the state
for the state
![]() is zero:
is zero:
![$\displaystyle \langle [A- \langle A \rangle ]^2 \rangle =
\frac{\langle \phi [...
...i \rangle }{\langle \phi \vert\phi\rangle}=0
\leadsto (A-a)\vert\phi \rangle=0.$](img845.png)
Axiom 2c:
The possible outcomes of measurements of an
observable corresponding to the hermitian linear operators ![]() are the eigenvalues of
are the eigenvalues of ![]() .
Immediately after the measurement, the quantum system is in the eigenstate of
.
Immediately after the measurement, the quantum system is in the eigenstate of ![]() corresponding to the
eigenvalue that is measured.
corresponding to the
eigenvalue that is measured.
This axiom is the most radical break with classical physics: it postulates an abrupt collapse of
the wave function (`reduction of the wave packet')
into one of the eigenstates of ![]() , if a measurement is performed.
Before the measurement is actually done, one can not predict its outcome, that is which eigenvalue
is measured. Only probabilities for the possible outcomes can be predicted:
, if a measurement is performed.
Before the measurement is actually done, one can not predict its outcome, that is which eigenvalue
is measured. Only probabilities for the possible outcomes can be predicted:
Axiom 2d:
Let ![]() have a complete system of eigenvectors
have a complete system of eigenvectors
![]() with eigenvalues
with eigenvalues ![]() .
The normalized
state
.
The normalized
state
![]() before the measurement of
before the measurement of ![]() can be expanded into
can be expanded into
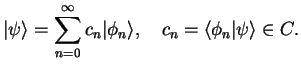 |
(195) |
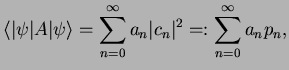 |
(196) |