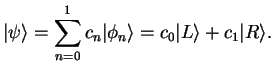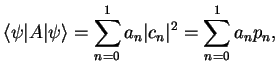Next: Energy Measurements
Up: Operators and Measurements
Previous: Eigenvalues and Measurement
Contents
We have seen above that a particle in the a double well
potential can be described by a vector
 in the Hilbert space
in the Hilbert space
 ,
,
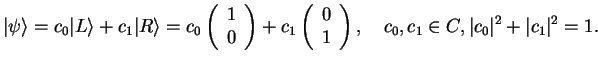 |
|
|
(197) |
The last condition
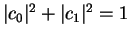 means that the state
means that the state
 is normalized.
What is the meaning of the coefficients
is normalized.
What is the meaning of the coefficients 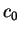 and
and 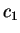 ?
?
CASE 1: 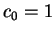 ,
, 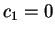 : The particle is in the state
: The particle is in the state
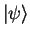 =
= 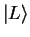 , which means
it is in the left well.
, which means
it is in the left well.
CASE 2: 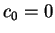 ,
, 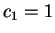 : The particle is in the state
: The particle is in the state
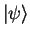 =
= 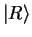 , which means
it is in the right well.
, which means
it is in the right well.
We define the operator (two-by-two matrix)
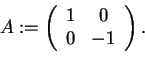 |
|
|
(198) |
Its eigenvectors are the two basis vector 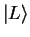 and
and 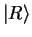 :
:
The operator 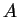 thus corresponds to the measurement `where is the particle, in the left or in the right well'.
This is the simplest version of a position measurement, where we are not interested in the precise position,
but only measure in which well the particle is. For example, if the particle is charged with the
elementary charge
thus corresponds to the measurement `where is the particle, in the left or in the right well'.
This is the simplest version of a position measurement, where we are not interested in the precise position,
but only measure in which well the particle is. For example, if the particle is charged with the
elementary charge 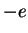 , we could measure the charge in the left well. If the particle is in there, we
find
, we could measure the charge in the left well. If the particle is in there, we
find 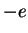 , if it is in the right well, we find 0.
, if it is in the right well, we find 0.
We now apply our axiom 2d to this `position measurement': we cite it here in the form that
exactly matches our two-level system:
Axiom 2d:
Let 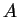 have a complete system of eigenvectors
have a complete system of eigenvectors
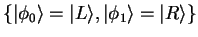 with eigenvalues
with eigenvalues
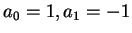 .
The normalized
state
.
The normalized
state
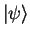 before the measurement of
before the measurement of 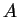 can be expanded into
can be expanded into
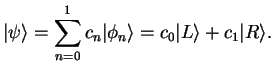 |
(200) |
Then, the expectation value of 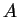 in
in
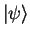 is
is
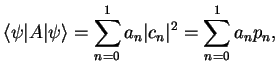 |
(201) |
and the probability 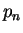 to find the system in the eigenstate
to find the system in the eigenstate
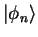 after the measurement is given by
the amplitude square
after the measurement is given by
the amplitude square
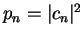 .
.
We therefore recognize:
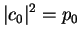 |
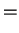 |
the probability to find the particle in the left well |
|
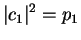 |
 |
the probability to find the particle in the right well |
(202) |
In particular, the probability to find the particle in either the left or the right well is
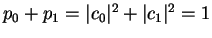 as it must be.
For example, if we perform the measurement by measuring an extra charge in the
left well, we find
as it must be.
For example, if we perform the measurement by measuring an extra charge in the
left well, we find 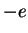 with probability
with probability 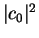 , and after the measurement the particle is
in the left well, that is in the state
, and after the measurement the particle is
in the left well, that is in the state 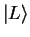 . If, on the other hand,
we find an extra charge 0 in the left well, the particle must be in the right well, that is in the
state
. If, on the other hand,
we find an extra charge 0 in the left well, the particle must be in the right well, that is in the
state 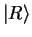 . The probability for this is
. The probability for this is
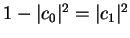 .
.




Next: Energy Measurements
Up: Operators and Measurements
Previous: Eigenvalues and Measurement
Contents
Tobias Brandes
2004-02-04
![]() in the Hilbert space
in the Hilbert space
![]() ,
,
![]() ,
, ![]() : The particle is in the state
: The particle is in the state
![]() =
= ![]() , which means
it is in the left well.
, which means
it is in the left well.
![]() ,
, ![]() : The particle is in the state
: The particle is in the state
![]() =
= ![]() , which means
it is in the right well.
, which means
it is in the right well.
![]() have a complete system of eigenvectors
have a complete system of eigenvectors
![]() with eigenvalues
with eigenvalues
![]() .
The normalized
state
.
The normalized
state
![]() before the measurement of
before the measurement of ![]() can be expanded into
can be expanded into