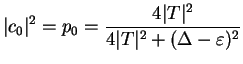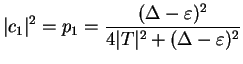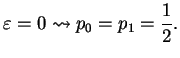Next: *Experiments in Double Quantum
Up: Energy Measurements
Previous: Eigenstates of the Two-Level
Contents
The measurement of the
total energy is a bit more complicated to do in practice than the position measurement.
For example, one can irradiate the system with light and measure an absorption peak
when the photon energy 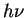 matches the energy difference
matches the energy difference 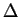 of the two levels.
After the absorption, the particle is in the excited state
of the two levels.
After the absorption, the particle is in the excited state 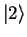 with energy
with energy
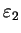 , before it was in its ground state
, before it was in its ground state 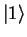 with energy
with energy
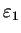 . The particle can go back into its ground state by, for example, spontaneous
emission of another photon of energy
. The particle can go back into its ground state by, for example, spontaneous
emission of another photon of energy 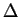 .
.
What we would like to find out now is the following: where is the particle, if it is in
its ground state 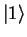 or its excited state
or its excited state 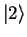 ? For example, after we perform
the absorption experiment and know that the particle is in its excited state, we would like
to find out if it is in the left or in the right well.
This means, we again perform a `position' measurement, and we can apply exactly the same argument
as before. The state before the position measurement is now the excited state
? For example, after we perform
the absorption experiment and know that the particle is in its excited state, we would like
to find out if it is in the left or in the right well.
This means, we again perform a `position' measurement, and we can apply exactly the same argument
as before. The state before the position measurement is now the excited state
Comparing the coefficients in front of the basis vectors 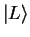 and
and 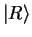 , we recognize:
, we recognize:
Again,
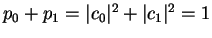 as it must be. This means: we can calculate in advance
the probability to find the particle in the left well after the absorption measurement, but
we can't tell where it is.
If we know that the particle is in its excited state
as it must be. This means: we can calculate in advance
the probability to find the particle in the left well after the absorption measurement, but
we can't tell where it is.
If we know that the particle is in its excited state 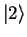 , but we haven't done the
position measurement yet, we still don't know if the particle is in the right or in the left
well. Its state
, but we haven't done the
position measurement yet, we still don't know if the particle is in the right or in the left
well. Its state 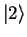 has components both in the left and the right well. For example,
if
has components both in the left and the right well. For example,
if
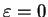 , we find
, we find
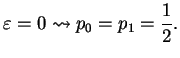 |
|
|
(209) |
In this case `it is completely unclear' where the particle is. Only the
subsequent position measurement can give us the answer: right with probability 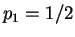 , and
left with probability
, and
left with probability 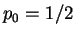 .
On the other hand, if the
coupling between the two wells is zero (in the case of an infinitely high barrier), we have
.
On the other hand, if the
coupling between the two wells is zero (in the case of an infinitely high barrier), we have 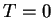 .
Then,
.
Then,
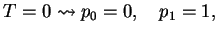 |
|
|
(210) |
which means that the particle is with certainty in the right well. This is obvious because for
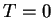 , the energy eigenstate
, the energy eigenstate
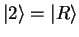 is simply the basis vector
is simply the basis vector 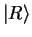 corresponding to the particle in the right well with probability one.
corresponding to the particle in the right well with probability one.




Next: *Experiments in Double Quantum
Up: Energy Measurements
Previous: Eigenstates of the Two-Level
Contents
Tobias Brandes
2004-02-04
![]() matches the energy difference
matches the energy difference ![]() of the two levels.
After the absorption, the particle is in the excited state
of the two levels.
After the absorption, the particle is in the excited state ![]() with energy
with energy
![]() , before it was in its ground state
, before it was in its ground state ![]() with energy
with energy
![]() . The particle can go back into its ground state by, for example, spontaneous
emission of another photon of energy
. The particle can go back into its ground state by, for example, spontaneous
emission of another photon of energy ![]() .
.
![]() or its excited state
or its excited state ![]() ? For example, after we perform
the absorption experiment and know that the particle is in its excited state, we would like
to find out if it is in the left or in the right well.
This means, we again perform a `position' measurement, and we can apply exactly the same argument
as before. The state before the position measurement is now the excited state
? For example, after we perform
the absorption experiment and know that the particle is in its excited state, we would like
to find out if it is in the left or in the right well.
This means, we again perform a `position' measurement, and we can apply exactly the same argument
as before. The state before the position measurement is now the excited state