



Next: The Two-Level System: Time-Evolution
Up: Energy Measurements
Previous: *Experiments in Double Quantum
Contents
Consider the operator
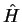 , the energy operator (Hamiltonian) for the infinite potential well
with the eigenstates
, the energy operator (Hamiltonian) for the infinite potential well
with the eigenstates 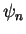 , Eq.(3.6),
If the state
, Eq.(3.6),
If the state 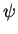 before the measurement is an eigenstate
before the measurement is an eigenstate
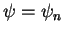 , measurement of the energy
yields the value
, measurement of the energy
yields the value 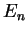 with probability
with probability
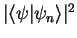 , that is with probability
1, and other values
, that is with probability
1, and other values 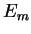 ,
, 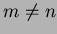 , with probability
, with probability
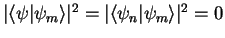 .
If the state
.
If the state 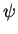 before the measurement is (cp. the problems)
the probability to obtain the value
before the measurement is (cp. the problems)
the probability to obtain the value 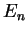 when measuring the energy is
In particular, we easily check (cp. the problems) that
as it must be.
when measuring the energy is
In particular, we easily check (cp. the problems) that
as it must be.
Tobias Brandes
2004-02-04
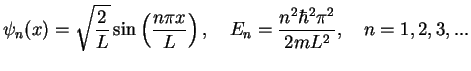
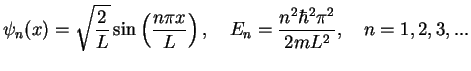
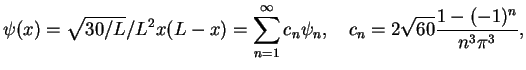
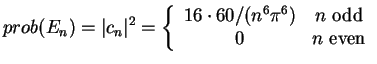
![$\displaystyle \sum_{n=0}^{\infty}prob(E_n)= [n=2k+1]=\sum_{k=1}^{\infty}\frac{16\cdot 60 }{(2k+1)^6\pi^6}=1
$](img956.png)