



Next: Important Quantum Mechanical Model
Up: The Two-Level System: Time-Evolution
Previous: The Two-Level System: Time-Evolution
Contents
To start with, we simply recall our first axiom of quantum mechanics here:
Axiom 1: A quantum mechanical system is described by a vector
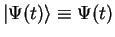 of a Hilbert space
of a Hilbert space 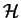 . The time evolution of
. The time evolution of 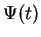 is determined by
the Schrödinger equation
is determined by
the Schrödinger equation
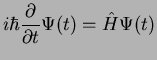 |
|
|
(211) |
The Hamilton operator 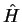 is an operator corresponding to the total
energy of the system.
The solutions of the stationary Schrödinger equation at fixed energy,
is an operator corresponding to the total
energy of the system.
The solutions of the stationary Schrödinger equation at fixed energy,
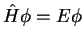 |
|
|
(212) |
are called stationary states, the possible energies  eigenenergies.
eigenenergies.
We now specialize everything to our two-level system:
| Hilbert space |
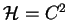 |
2d complex vector space |
| Basis vectors |
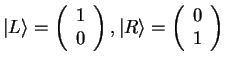 |
particle left or right |
| Arbitrary vector |
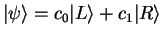 , ,
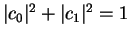 |
particle in arbitrary state |
| Hamiltonian |
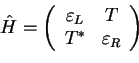 |
two-dimensional matrix |
| Stationary states |
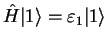 , ,
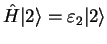 |
The two energy eigenstates |
Time evolution means the following: Suppose the state of the quantum system at time 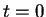 is
is
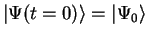 . Then,
the solution of the time-dependent Schrödinger equation
. Then,
the solution of the time-dependent Schrödinger equation
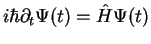 gives us the state
gives us the state
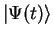 at a later time
at a later time 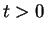 .
.
CASE 1: Time evolution of a stationary state
If the initial state
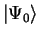 is a stationary state, the time-evolution is simple:
is a stationary state, the time-evolution is simple:
because
(the same for
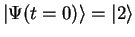 ). The time-evolution is `trivial' and
just given by the phase factor
). The time-evolution is `trivial' and
just given by the phase factor
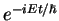 , where
, where  is the eigenenergy of the
stationary state.
is the eigenenergy of the
stationary state.
CASE 2: Time evolution of a superposition of the two energy eigenstates
because
To obtain the time evolution of an arbitrary initial state
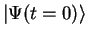 , we therefore
have to do the following: decompose
, we therefore
have to do the following: decompose
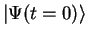 into a linear combination of
energy eigenstates (
into a linear combination of
energy eigenstates (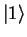 and
and 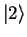 ). Then, simply dress the stationary
states in this linear combination with the phase factors
). Then, simply dress the stationary
states in this linear combination with the phase factors
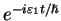 and
and
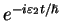 . The linearity of the Schrödinger equation makes it that simple:
the time evolution of a sum of stationary states is the sum of the time-evolved
linear components of this sum.
. The linearity of the Schrödinger equation makes it that simple:
the time evolution of a sum of stationary states is the sum of the time-evolved
linear components of this sum.
The calculational effort is in the determination of the coefficients 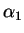 and
and
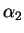 : we discuss this in the special
: we discuss this in the special
CASE 3: The initial state is
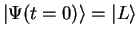 , describing the particle
in the left well. Note that we don't have simply a time evolution given by a phase factor:
, describing the particle
in the left well. Note that we don't have simply a time evolution given by a phase factor:
The state 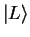 is not an eigenstate of the Hamiltonian
is not an eigenstate of the Hamiltonian 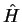 , therefore its time evolution
is not given by a simple phase factor.
What we have to do is clear: we have to find the decomposition of the vector
, therefore its time evolution
is not given by a simple phase factor.
What we have to do is clear: we have to find the decomposition of the vector 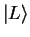 into
a linear combination of energy eigenstates
into
a linear combination of energy eigenstates 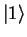 and
and 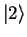 ,
,
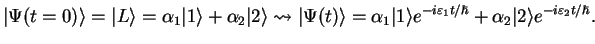 |
|
|
(217) |
For simplicity, we do this for the special case of negative 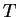 and identical
energy parameters
and identical
energy parameters
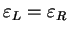 in the Hamiltonian
in the Hamiltonian 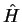 . We had calculated already
before in (3.41),
. We had calculated already
before in (3.41),
We solve this equation for 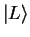 ,
,
By this we have found our desired result, that is the time evolution of the initial
state 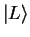 ,
,
We have expressed
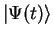 in the basis of the energy eigenstates
in the basis of the energy eigenstates 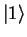 and
and
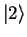 . We now would like to express
. We now would like to express
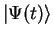 in the basis of the
left and right states,
in the basis of the
left and right states, 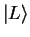 and
and 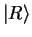 : this is simple because we
know
: this is simple because we
know
The coefficients 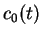 and
and 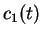 have a clear physical meaning: let us recall
have a clear physical meaning: let us recall
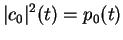 |
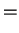 |
the probability to find the particle in the left well |
|
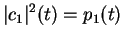 |
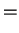 |
the probability to find the particle in the right well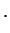 |
(222) |
Obviously, these probabilities are a function of time now:
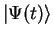 is not stationary.
We calculate
is not stationary.
We calculate
and therefore
![$\displaystyle \cos^2 [\frac{(\varepsilon_1-\varepsilon_2)t}{2\hbar}]$](img1005.png) |
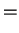 |
the probability to find the particle in the left well |
|
![$\displaystyle \sin^2 [\frac{(\varepsilon_1-\varepsilon_2)t}{2\hbar}]$](img1008.png) |
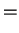 |
the probability to find the particle in the right well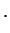 |
(224) |
As a function of time, the probabilities oscillate with an angular frequency that is given by the
energy splitting
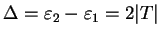 , divided by
, divided by 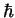 . At the initial time
. At the initial time
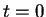 , the particle is in the left well (the probability
, the particle is in the left well (the probability 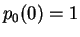 ), but for
), but for 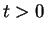 this
probability starts to oscillate: the particle tunnels from the left well into the right well, back into
the left well and so forth.
this
probability starts to oscillate: the particle tunnels from the left well into the right well, back into
the left well and so forth.




Next: Important Quantum Mechanical Model
Up: The Two-Level System: Time-Evolution
Previous: The Two-Level System: Time-Evolution
Contents
Tobias Brandes
2004-02-04
![]() of a Hilbert space
of a Hilbert space ![]() . The time evolution of
. The time evolution of ![]() is determined by
the Schrödinger equation
is determined by
the Schrödinger equation
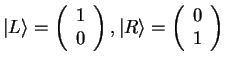
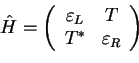
![]() is
is
![]() . Then,
the solution of the time-dependent Schrödinger equation
. Then,
the solution of the time-dependent Schrödinger equation
![]() gives us the state
gives us the state
![]() at a later time
at a later time ![]() .
.
![]() is a stationary state, the time-evolution is simple:
is a stationary state, the time-evolution is simple:
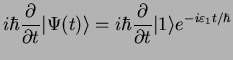
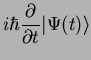
![$\displaystyle i\hbar \frac{\partial}{\partial t}\left[\alpha_1
\vert 1\rangle e...
...repsilon_1 t/\hbar}
+\alpha_2 \vert 2\rangle e^{-i\varepsilon_2 t/\hbar}\right]$](img974.png)
![]() and
and
![]() : we discuss this in the special
: we discuss this in the special
![]() , describing the particle
in the left well. Note that we don't have simply a time evolution given by a phase factor:
, describing the particle
in the left well. Note that we don't have simply a time evolution given by a phase factor:
![$\displaystyle \frac{1}{\sqrt{2}}\left[ \vert 1\rangle - \vert 2\rangle \right]\leadsto
\alpha_1 = \frac{1}{\sqrt{2}},\quad \alpha_2 = -\frac{1}{\sqrt{2}}.$](img988.png)
![$\displaystyle \frac{1}{\sqrt{2}}\left[\vert L\rangle + \vert R\rangle \right],\...
...rt 2\rangle = \frac{1}{\sqrt{2}}\left[ -\vert L\rangle + \vert R\rangle \right]$](img991.png)
![$\displaystyle \frac{1}{\sqrt{2}}\left[ \vert 1\rangle e^{-i\varepsilon_1 t/\hbar}
- \vert 2\rangle e^{-i\varepsilon_2 t/\hbar}\right] =$](img993.png)
![$\displaystyle \frac{1}{{2}}\left\{ \left[\vert L\rangle + \vert R\rangle \right...
...[-\vert L\rangle + \vert R\rangle \right] e^{-i\varepsilon_2 t/\hbar}\right\} =$](img994.png)
![$\displaystyle \frac{1}{{2}}\left\{\vert L\rangle \left[e^{-i\varepsilon_1 t/\hb...
... \left[e^{-i\varepsilon_1 t/\hbar} - e^{-i\varepsilon_2 t/\hbar}\right]\right\}$](img995.png)
![$\displaystyle \frac{1}{{2}}\left[e^{-i\varepsilon_1 t/\hbar} + e^{-i\varepsilon...
...{1}{{2}}\left[e^{-i\varepsilon_1 t/\hbar} - e^{-i\varepsilon_2 t/\hbar}\right].$](img998.png)
![$\displaystyle \frac{1}{{4}}\left\vert e^{-i\varepsilon_1 t/\hbar} + e^{-i\varep...
...2
=\frac{1}{2}\left\{ 1 + \cos [(\varepsilon_1-\varepsilon_2)t/\hbar)] \right\}$](img1004.png)
![$\displaystyle \cos^2 [\frac{(\varepsilon_1-\varepsilon_2)t}{2\hbar}]$](img1005.png)
![$\displaystyle \frac{1}{{4}}\left\vert e^{-i\varepsilon_1 t/\hbar} - e^{-i\varep...
...2
=\frac{1}{2}\left\{ 1 - \cos [(\varepsilon_1-\varepsilon_2)t/\hbar)] \right\}$](img1007.png)
![$\displaystyle \sin^2 [\frac{(\varepsilon_1-\varepsilon_2)t}{2\hbar}]$](img1008.png)
![$\displaystyle \cos^2 [\frac{(\varepsilon_1-\varepsilon_2)t}{2\hbar}]$](img1005.png)
![$\displaystyle \sin^2 [\frac{(\varepsilon_1-\varepsilon_2)t}{2\hbar}]$](img1008.png)