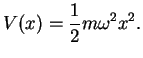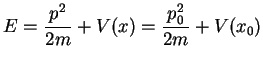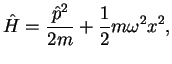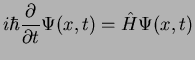Next: Solution of the Differential
Up: The Harmonic Oscillator I
Previous: The Harmonic Oscillator I
Contents
The one-dimensional harmonic oscillator is defined by a quadratic potential 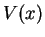 that for convenience
is chosen to be symmetric to the origin,
that for convenience
is chosen to be symmetric to the origin,
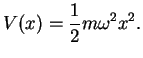 |
|
|
(225) |
Here, 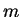 is the mass of the particle and
is the mass of the particle and 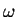 the parameter that determines the shape of the parabola.
We wish to determine the behaviour of a particle of mass
the parameter that determines the shape of the parabola.
We wish to determine the behaviour of a particle of mass 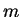 in this potential.
In classical (Newtonian) physics, all one would have to do would be to solve Newton's equations
for a given initial position
in this potential.
In classical (Newtonian) physics, all one would have to do would be to solve Newton's equations
for a given initial position 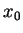 and a given initial momentum
and a given initial momentum 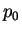 at time
at time 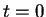 to determine
to determine 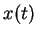 and
and 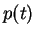 at a later time
at a later time 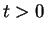 . The total energy
. The total energy
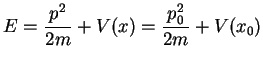 |
|
|
(226) |
is constant and determines an ellipse in phase space. The particle starts at the point 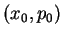 on this
ellipse and then moves on this ellipse. Of course, as a function of time
on this
ellipse and then moves on this ellipse. Of course, as a function of time 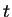 we can easily solve
for
we can easily solve
for 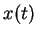 by solving the differential equation (Newton's law)
by solving the differential equation (Newton's law)
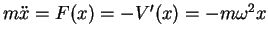 .
.
In quantum mechanics, we have the total energy replaces by the Hamilton operator (Hamiltonian)
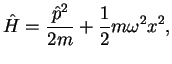 |
|
|
(227) |
and we have to solve the time-dependent Schrödinger equation
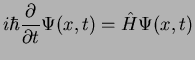 |
|
|
(228) |
for a given initial wave function 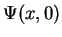 . We have learned that this can be achieved by first solving the
stationary Schrödinger equation
. We have learned that this can be achieved by first solving the
stationary Schrödinger equation
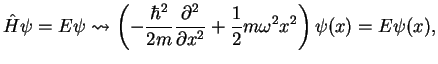 |
|
|
(229) |
which is an equation for the possible energy eigenvalues  and eigenfunctions
and eigenfunctions 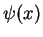 . The eigenfunctions
are useful themselves as they provide inside into the possible states the particle can be in. We have also learned that
the eigenfunctions provide a basis into which the initial wave function
. The eigenfunctions
are useful themselves as they provide inside into the possible states the particle can be in. We have also learned that
the eigenfunctions provide a basis into which the initial wave function 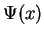 can be expanded and thus the
time-evolution of an arbitrary initial wave function can be obtained.
can be expanded and thus the
time-evolution of an arbitrary initial wave function can be obtained.




Next: Solution of the Differential
Up: The Harmonic Oscillator I
Previous: The Harmonic Oscillator I
Contents
Tobias Brandes
2004-02-04