



Next: The Harmonic Oscillator II
Up: The Harmonic Oscillator I
Previous: Model
Contents
Now we actually want to solve (4.5). We introduce dimensionless quantities
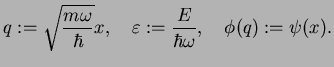 |
|
|
(230) |
Then, (4.5) becomes
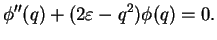 |
|
|
(231) |
For large
 , one can neglect the term
, one can neglect the term
 . This yields the asymptotic behaviour of
. This yields the asymptotic behaviour of
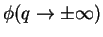 ,
,
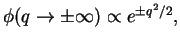 |
|
|
(232) |
which you can check by differentiating
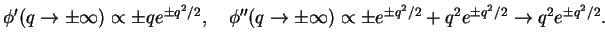 |
|
|
(233) |
This roughly is an example of how an asymptotic analysis of a differential equation
is performed; if you are interested for more mathematical details of the interesting
theory of asymptotic analysis have a look at the book by Bender and Orszag.
We obviously have two different solutions: one grows to infinity as
 , while the
other goes to zero. Wave functions have to be normalized which is impossible for the solution
that grows to infinity. We exclude that solution and write
, while the
other goes to zero. Wave functions have to be normalized which is impossible for the solution
that grows to infinity. We exclude that solution and write 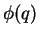 as
as
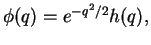 |
|
|
(234) |
which is an ANSATZ with an up to now unknown function 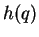 that we wish to determine. To do so, we
plug it into our differential equation (4.7) and use
that we wish to determine. To do so, we
plug it into our differential equation (4.7) and use
which leads to
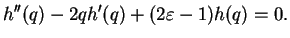 |
|
|
(236) |
We try to solve this by a power series
We insert these series into (4.12),
![$\displaystyle \sum_{k=0}^{\infty}\left[
(k+1)(k+2)a_{k+2} -2k a_k +(2\varepsilon -1)a_k
\right]q^k=0.$](img1044.png) |
|
|
(238) |
The left side of the equation must be zero for any value of 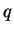 which can only be true if
all the coefficients in
which can only be true if
all the coefficients in ![$ [...]$](img1046.png) vanish. The powers
vanish. The powers 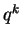 form an infinite basis
form an infinite basis
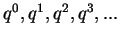 ;
if any function expanded in this basis is zero, all expansion coefficients must be zero. From
;
if any function expanded in this basis is zero, all expansion coefficients must be zero. From
![$ [...]=0$](img1049.png) in (4.14), we therefore have
in (4.14), we therefore have
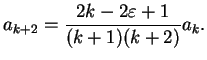 |
|
|
(239) |
This is a recursion relation for the coefficients 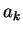 .
For large
.
For large
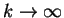 , one has
, one has
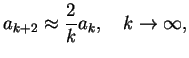 |
|
|
(240) |
unless the 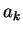 become zero above some
become zero above some 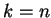 .
The infinite power series
.
The infinite power series 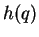 becomes asymptotical equal to the exponential function
becomes asymptotical equal to the exponential function
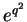 for large
for large 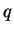 : consider
: consider
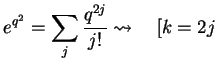 even even![$\displaystyle ]
\frac{a_{k+2}}{a_k}=\frac{(k/2)!}{(k/2+1)!}=\frac{1}{k/2+1}\to \frac{2}{k},\quad k\to \infty.$](img1057.png) |
|
|
(241) |
Now, this is obviously not what we had intended
with our Ansatz, because this would mean that the wave function
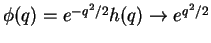 which means
that it is no longer normalizable. The only possibility for a solution
which means
that it is no longer normalizable. The only possibility for a solution 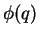 that
vanishes as
that
vanishes as
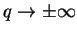 therefore is obtained by demanding that the
therefore is obtained by demanding that the
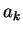 become zero above some
become zero above some 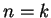 whence
whence 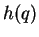 becomes a polynomial of finite degree.
For this to be the case, the numerator
in (4.15) has to vanish for some
becomes a polynomial of finite degree.
For this to be the case, the numerator
in (4.15) has to vanish for some 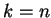 which means
which means
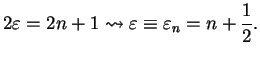 |
|
|
(242) |
The possible energy values  are therefore
are therefore
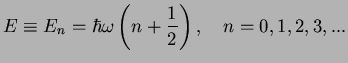 |
|
|
(243) |
This is the famous quantization of the energy of the harmonic oscillator, which Planck had
postulated to explain the blackbody radiation in 1900!
For each non-negative integer 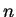 we obtain one energy eigenvalue and
the corresponding eigenfunction
we obtain one energy eigenvalue and
the corresponding eigenfunction
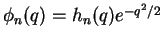 from the finite recursion formula (4.15) for the polynomial
from the finite recursion formula (4.15) for the polynomial 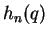 .
Here, we already use the index
.
Here, we already use the index 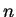 to denote the
to denote the 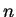 -th solution.
The polynomials
-th solution.
The polynomials 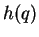 fulfill the differential equation (4.12) with
fulfill the differential equation (4.12) with
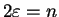 , that is
, that is
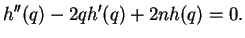 |
|
|
(244) |
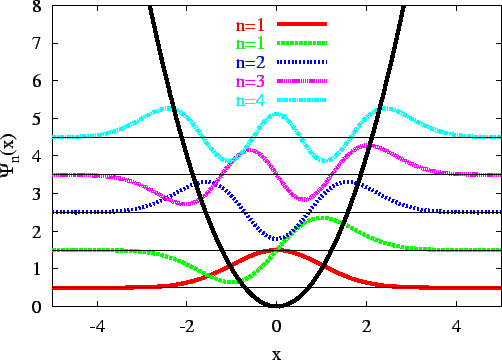
Figure:
Lowest eigenstate wave functions  , Eq.(4.21) of the
one-dimensional harmonic oscillator potential
, Eq.(4.21) of the
one-dimensional harmonic oscillator potential
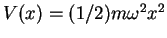 (black curve).
Wave functions are in units
(black curve).
Wave functions are in units
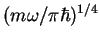 . The curves have an offset for clarity.
. The curves have an offset for clarity.
 |
The polynomials 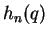 that fulfill (4.20)
are called Hermite polynomials
that fulfill (4.20)
are called Hermite polynomials 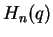 if they are normalized such that the
wavefunctions
if they are normalized such that the
wavefunctions
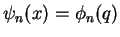 are normalized: the result for the
normalized eigenfunctions
are normalized: the result for the
normalized eigenfunctions 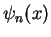 with eigenenergy
with eigenenergy 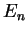 , that is the solutions of (4.5),
is
, that is the solutions of (4.5),
is
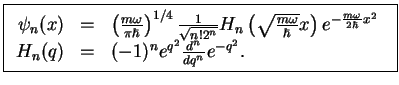 |
|
|
(245) |
We do not prove the explicit form of the Hermite polynomials here; in the next section we will
learn an alternative method to calculate the 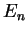 and the
and the 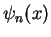 anyway.
Here, we calculate
anyway.
Here, we calculate 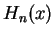 for the first
for the first 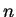 , using (4.21) (denote
, using (4.21) (denote 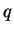 by
by 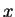 here)
here)
The lowest eigenfuncions 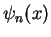 are shown in Fig. (4.1).
are shown in Fig. (4.1).




Next: The Harmonic Oscillator II
Up: The Harmonic Oscillator I
Previous: Model
Contents
Tobias Brandes
2004-02-04
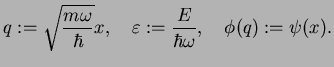
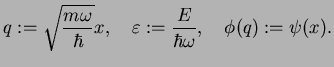
![]() , while the
other goes to zero. Wave functions have to be normalized which is impossible for the solution
that grows to infinity. We exclude that solution and write
, while the
other goes to zero. Wave functions have to be normalized which is impossible for the solution
that grows to infinity. We exclude that solution and write ![]() as
as
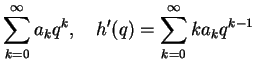
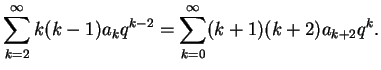
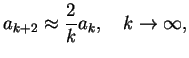
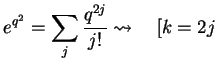 even
even![$\displaystyle ]
\frac{a_{k+2}}{a_k}=\frac{(k/2)!}{(k/2+1)!}=\frac{1}{k/2+1}\to \frac{2}{k},\quad k\to \infty.$](img1057.png)
![]() which means
that it is no longer normalizable. The only possibility for a solution
which means
that it is no longer normalizable. The only possibility for a solution ![]() that
vanishes as
that
vanishes as
![]() therefore is obtained by demanding that the
therefore is obtained by demanding that the
![]() become zero above some
become zero above some ![]() whence
whence ![]() becomes a polynomial of finite degree.
For this to be the case, the numerator
in (4.15) has to vanish for some
becomes a polynomial of finite degree.
For this to be the case, the numerator
in (4.15) has to vanish for some ![]() which means
which means
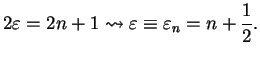
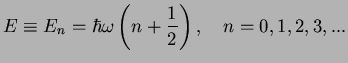
![]() we obtain one energy eigenvalue and
the corresponding eigenfunction
we obtain one energy eigenvalue and
the corresponding eigenfunction
![]() from the finite recursion formula (4.15) for the polynomial
from the finite recursion formula (4.15) for the polynomial ![]() .
Here, we already use the index
.
Here, we already use the index ![]() to denote the
to denote the ![]() -th solution.
The polynomials
-th solution.
The polynomials ![]() fulfill the differential equation (4.12) with
fulfill the differential equation (4.12) with
![]() , that is
, that is
