



Next: Harmonic Oscillator Hilbert Space
Up: The Hilbert space of
Previous: The Hilbert space of
Contents
Let us recall what we know from the infinite potential well:
The eigen functions 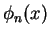 of the infinite potential well form the basis
of a linear vector space
of the infinite potential well form the basis
of a linear vector space
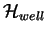 of functions
of functions 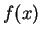 defined on the
interval
defined on the
interval ![$ [0,L]$](img379.png) with
with
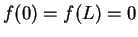 .
The
.
The 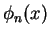 form an orthonormal basis:
form an orthonormal basis:
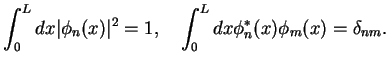 |
|
|
(249) |
(We can omit the 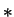 here because the
here because the 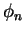 are real).
Note that the orthonormal basis is of infinite dimension because there are infinitely many
are real).
Note that the orthonormal basis is of infinite dimension because there are infinitely many
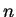 . The infinite dimension of the vector space (function space)
. The infinite dimension of the vector space (function space)
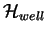 is the main difference to ordinary, finite dimensional vector spaces
like the
is the main difference to ordinary, finite dimensional vector spaces
like the 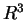 .
Any function
.
Any function
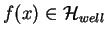 (like any arbitrary vector in, e.g., the vector space
(like any arbitrary vector in, e.g., the vector space 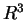 ) can be expanded into
a linear combination of basis `vectors', i.e. eigen functions
) can be expanded into
a linear combination of basis `vectors', i.e. eigen functions 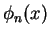 :
:
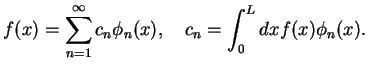 |
|
|
(250) |
We start to count the eigenstates from 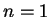 .
.




Next: Harmonic Oscillator Hilbert Space
Up: The Hilbert space of
Previous: The Hilbert space of
Contents
Tobias Brandes
2004-02-04
![]() of the infinite potential well form the basis
of a linear vector space
of the infinite potential well form the basis
of a linear vector space
![]() of functions
of functions ![]() defined on the
interval
defined on the
interval ![]() with
with
![]() .
The
.
The ![]() form an orthonormal basis:
form an orthonormal basis: