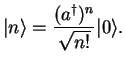Next: The Harmonic Oscillator
Up: Ladder Operators, Phonons and
Previous: Ladder Operators, Phonons and
Contents
We define the two operators
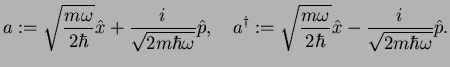 |
|
|
(263) |
You have showed in the problems that if two operators 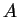 and
and 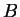 are hermitian,
are hermitian,
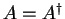 ,
,
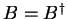 the linear combination
the linear combination 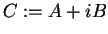 is not hermitian but
is not hermitian but
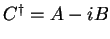 (remember the analogy
to a complex number
(remember the analogy
to a complex number
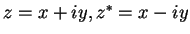 ).
We know that
).
We know that 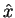 and
and 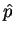 are hermitian, therefore
are hermitian, therefore
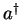 (`a dagger') is the hermitian
conjugate of
(`a dagger') is the hermitian
conjugate of 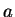 .
From the commutator of
.
From the commutator of 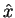 and
and 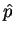 we easily find (see the problems)
we easily find (see the problems)
![$\displaystyle [\hat{x},\hat{p}]=i\hbar\leadsto [a,a^{\dagger}] = 1.$](img1127.png) |
|
|
(264) |
We define the number operator
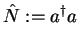 |
|
|
(265) |
which is a hermitian operator because
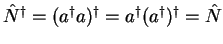 .
The eigenvalues of
.
The eigenvalues of 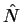 must be real therefore. We denote the eigenvalues of
must be real therefore. We denote the eigenvalues of
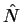 by
by 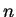 and show that the
and show that the 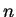 are non-negative integers: First, we denote the
corresponding (normalized) eigenvectors of
are non-negative integers: First, we denote the
corresponding (normalized) eigenvectors of 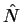 by
by 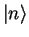 ,
,
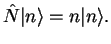 |
|
|
(266) |
STEP 1: We show 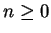 : remember the scalar product of
two states
: remember the scalar product of
two states
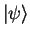 and
and
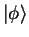 is denoted as
is denoted as
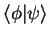 .
.
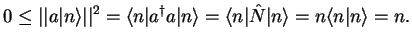 |
|
|
(267) |
STEP 2: We step down the ladder: if 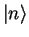 is an eigenvector of
is an eigenvector of 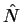 with eigenvalue
with eigenvalue
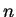 , then
, then
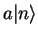 is an eigenvector of
is an eigenvector of 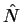 with eigenvalue
with eigenvalue 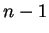 ,
,
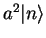 is an eigenvector of
is an eigenvector of 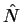 with eigenvalue
with eigenvalue 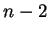 ,
,
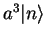 is an eigenvector of
is an eigenvector of 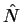 with eigenvalue
with eigenvalue 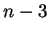 ,...
,...
The state
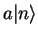 is an eigenstate of
is an eigenstate of 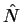 with eigenvalue
with eigenvalue 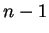 and therefore must be proportional
to
and therefore must be proportional
to
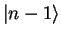 ,
,
The operator 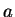 takes us from one eigenstate with eigenvalue
takes us from one eigenstate with eigenvalue 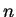 to a lower eigenstate with
eigenvalue
to a lower eigenstate with
eigenvalue 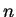
STEP 3: We show that 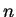 must be an integer, and the only possile eigenstates of
must be an integer, and the only possile eigenstates of 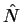 are
are 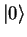 ,
, 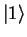 ,
, 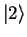 , ...
, ...
If we step down the ladder to lower and lower eigenvalues,
we eventually would come to negative eigenvalues which can't be
because all eigenvalues of 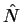 must be non-negative! The lowest possible eigenstate is
must be non-negative! The lowest possible eigenstate is
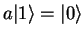 with eigenvalue 0:
with eigenvalue 0:
For any 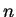 with
with 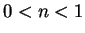 , the eigenvalue equation
, the eigenvalue equation
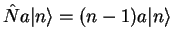 can only be true if
can only be true if
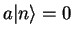 is the zero-vector. It then becomes the trivial equation
is the zero-vector. It then becomes the trivial equation
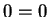 that contains no contradictions. But
that contains no contradictions. But
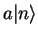 cannot be the zero-vector because
the norm of
cannot be the zero-vector because
the norm of
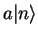 is
is
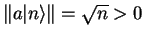 . Therefore,
. Therefore, 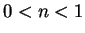 leads to a contradition. In the same way,
there can't be values of
leads to a contradition. In the same way,
there can't be values of 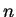 with
with 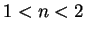 (application of
(application of  leads us to the case
leads us to the case 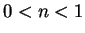 which is
already excluded. As a result, n is an integer.
which is
already excluded. As a result, n is an integer.
Step 4:
The normalized state
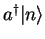 is (the proof is left for the problems)
is (the proof is left for the problems)
Therefore,
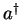 takes us up the ladder from one eigenstate
takes us up the ladder from one eigenstate 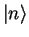 to the next higher
to the next higher
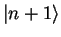 .
All the normalized eigenstates
.
All the normalized eigenstates 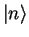 can be created from the ground state
can be created from the ground state 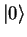 by successive
application of the ladder operator
by successive
application of the ladder operator
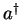 :
:
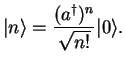 |
|
|
(271) |




Next: The Harmonic Oscillator
Up: Ladder Operators, Phonons and
Previous: Ladder Operators, Phonons and
Contents
Tobias Brandes
2004-02-04
![$\displaystyle a^{\dagger}aa= \left( aa^ {\dagger}- [a,a^{\dagger}]\right) a =
\left( aa^ {\dagger}- 1\right) a =
a \left( \hat{N}- 1 \right)$](img1143.png)
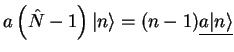
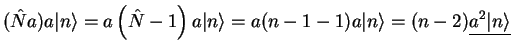
![]() must be an integer, and the only possile eigenstates of
must be an integer, and the only possile eigenstates of ![]() are
are ![]() ,
, ![]() ,
, ![]() , ...
, ...
![]() must be non-negative! The lowest possible eigenstate is
must be non-negative! The lowest possible eigenstate is
![]() with eigenvalue 0:
with eigenvalue 0:
![]() is (the proof is left for the problems)
is (the proof is left for the problems)