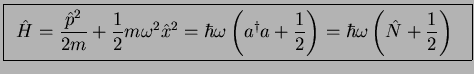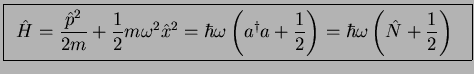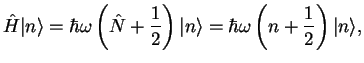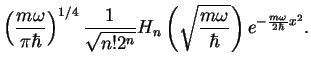Next: Phonons and Photons
Up: Ladder Operators, Phonons and
Previous: The Ladder Operators and
Contents
The connection of the above algebraic tour de force
with the harmonic oscillator is very simple: The Hamiltonian (4.38)
can be written as
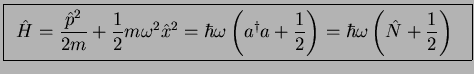 |
|
|
(272) |
which you can check by inserting the definitions of 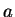 and
and
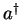 .
The eigenvectors of
.
The eigenvectors of 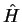 are the eigenvectors of
are the eigenvectors of 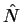 :
:
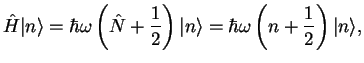 |
|
|
(273) |
from which we can read off the eigenvalues of the harmonic oscillator,
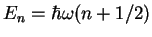 . The corresponding
eigenfunctions are, of course, the eigenfunctions of the harmonic oscillator,
. The corresponding
eigenfunctions are, of course, the eigenfunctions of the harmonic oscillator,
This is not so easy to see directly; it is proofed for the ground state 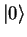 in the problems.
in the problems.




Next: Phonons and Photons
Up: Ladder Operators, Phonons and
Previous: The Ladder Operators and
Contents
Tobias Brandes
2004-02-04