



Next: The Hydrogen Atom
Up: Ladder Operators, Phonons and
Previous: The Harmonic Oscillator
Contents
We call the state 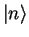 of the harmonic oscillator with energy
of the harmonic oscillator with energy
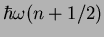 a state with
a state with 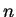 quanta
quanta
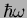 of energy plus the
zero point energy
of energy plus the
zero point energy
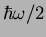 . These quanta are called phonons
for systems where massive particles have oscillatory degrees of freedom,
the state
. These quanta are called phonons
for systems where massive particles have oscillatory degrees of freedom,
the state 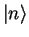 is a
is a 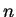 -phonon state.
-phonon state.
The ladder operator
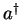 operates as
operates as
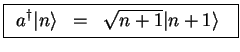 |
|
|
(276) |
and creates a state with one more phonon which is why it is called a creation operator.
In the same way, the operator 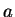 ,
,
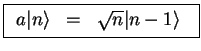 |
|
|
(277) |
leads to a state with one phonon less (it destroys one phonon) and is called a
annihilation operator.
In a similar manner, the oscillatory degrees of freedom of the electromagnetic field
(light) lead to a Hamiltonian like the one of the harmonic oscillator. The corresponding states
are called  -photon states.
This is one of the topics of Quantum Mechanics II, the theory of light, and many-body theory.
It is there where operators like the
-photon states.
This is one of the topics of Quantum Mechanics II, the theory of light, and many-body theory.
It is there where operators like the 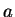 and
and 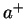 show their full versatility and power.
show their full versatility and power.




Next: The Hydrogen Atom
Up: Ladder Operators, Phonons and
Previous: The Harmonic Oscillator
Contents
Tobias Brandes
2004-02-04
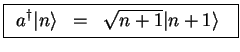
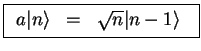
![]() -photon states.
This is one of the topics of Quantum Mechanics II, the theory of light, and many-body theory.
It is there where operators like the
-photon states.
This is one of the topics of Quantum Mechanics II, the theory of light, and many-body theory.
It is there where operators like the ![]() and
and ![]() show their full versatility and power.
show their full versatility and power.