



Next: The Angular Part
Up: Spherical Symmetric Potentials in
Previous: The Potential
Contents
It is useful to introduce polar coordinates
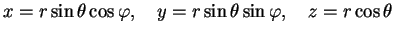 |
|
|
(282) |
and to re-write the Laplacian in polar coordinates,
![$\displaystyle \Delta \Psi= \frac{1}{r^2}\frac{\partial}{\partial r}\left(r^2
\f...
...ight)
+\frac{1}{\sin^2 \theta}\frac{\partial^2\Psi}{\partial \varphi^2}\right].$](img1192.png) |
|
|
(283) |
The wave function
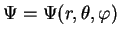 now depends on polar coordinates. We multiply
the Schrödinger equation with
now depends on polar coordinates. We multiply
the Schrödinger equation with 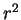 ,
,
which can be written with two operators 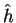 and
and
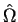 as
as
The separation of 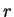 -dependences and angle dependences suggests a separation Ansatz, that is
a wave function of the form
-dependences and angle dependences suggests a separation Ansatz, that is
a wave function of the form
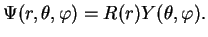 |
|
|
(284) |
Then,
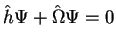 means
means
Here, we have used the fact that 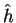 performs a
differentiation with respect to
performs a
differentiation with respect to 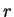 so that
so that
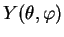 can be pulled in front of it. In the same way,
can be pulled in front of it. In the same way,
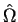 performs a differentiation with respect to
performs a differentiation with respect to 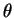 and
and 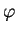 only
so that
only
so that 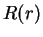 can be pulled in front of it. We thus have succeeded to completely seperate
the radial part
can be pulled in front of it. We thus have succeeded to completely seperate
the radial part 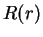 from the angular part
from the angular part
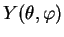 . The left side in
(4.62) depends only on
. The left side in
(4.62) depends only on 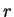 , the right side only on
, the right side only on
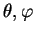 whence both side must be
a constant that we have denoted for convenience as
whence both side must be
a constant that we have denoted for convenience as 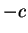 here.
here.
We first investigate the angular part as it can be solved exactly. The radial
part can not be solved exactly for an arbitrary potential 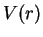 .
.




Next: The Angular Part
Up: Spherical Symmetric Potentials in
Previous: The Potential
Contents
Tobias Brandes
2004-02-04
![$\displaystyle \Delta \Psi= \frac{1}{r^2}\frac{\partial}{\partial r}\left(r^2
\f...
...ight)
+\frac{1}{\sin^2 \theta}\frac{\partial^2\Psi}{\partial \varphi^2}\right].$](img1192.png)
![$\displaystyle \frac{\partial}{\partial r}\left(r^2
\frac{\partial \Psi}{\partia...
...ht)
+\frac{1}{\sin^2 \theta}\frac{\partial^2\Psi}{\partial \varphi^2}\right]=0,$](img1195.png)
![]() .
.