Overview of the mesoscopic theory of liquid crystals
What are liquid crystals and why are they interesting?
Before we concentrate on the thermodynamics of liquid crystals we
shall give some brief introductory remarks. A liquid crystal consists of
form-anisotropic particles which show long-range correlations with
respect to the orientation of their molecular axes, but which are still able
to flow and posses no or only weak long-range correlations with
respect to their centers of mass.
Both phenomena together lead to a
fluid-like material possessing crystal-like properties. The first
liquid crystal was reported in 1888 in a letter from Lehmann to
Reinitzer, both of them becoming interested in these new
materials. Why now should orientational order result in crystal-like
properties like birefringence? The answer is
connected with the
molecular structure of the material. Let us look at a typical liquid
crystals like MBBA –
n-4'-methoxybenzylidene-n-butylanilin.
This is maybe the most prominent liquid crystal (but
not the first known), even if industrial use of liquid crystals is
usually made of mixtures
of many different substances. The
space filling model is shown in Fig. 1.
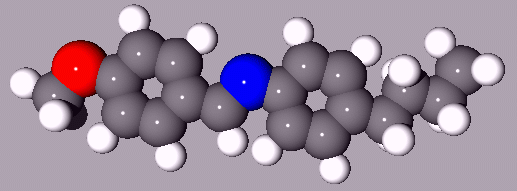
Figure 1: Structural formula and space filling model of
MBBA. Note the conjugated double
bonds and the "smeared" system of pi-electrons along the long axis of the
molecule.
First of all the molecule is rather stiff and possesses an axis ratio of
2.5 (accounting for the form-anisotropy). In addition the conjugated
double bonds yield a large pi-electron system distributed along the
long axis of the molecule. Thus polarizability differs considerably
parallel to the long axes and perpendicular to it. Since the
dielectric constant of
the material is an ensemble average over all
molecules in a volume element the dielectric constant depends clearly on the
orientational distribution of the
molecules and so does the refraction index. Hence the optical
properties depend on direction and
polarization of the incident ray, and the material shows
birefringence.
It is clear that such materials are not only of academic interest but
provide lots of interesting applications (displays, optical switches,
and much more).
A typical phase sequence (this is rather simplified and not
valid in general: some liquid crystal show a cholesteric
phase or much more smectic phases) of
a liquid crystal is shown in Fig. 2.
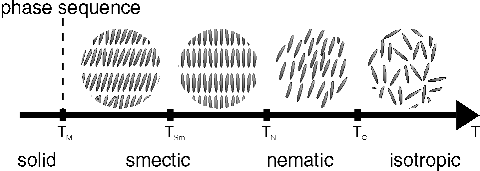
Figure 2: Schematical phase sequence of a liquid
crystal. From left to right: smectic C phase
(tilt angle between layer normal and mean orientation of the
molecules), smectic A phase (layered structure, no tilt), nematic
phase, isotropic phase
Above the clearing temperature Tc the
liquid crystal becomes an
isotropic liquid. These properties make
liquid crystals an interesting object for the application of
thermodynamical methods. However, the practical importance of these
materials is due to applications which take advantage of the
orientational order in the fluid: we shall come back to that later.
Configuration space and orientation distribution function
The additional degrees of freedom in a liquid crystal
are the orientations of the particles. However, in most cases the
distinction between head and tail of these constituents is artificial,
and we end up with the unit sphere with antipodal points identified as
parameter space. Thus we describe
the liquid crystal with the help of the nematic space
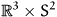 . On this space we introduce the orientational mass
density
. On this space we introduce the orientational mass
density
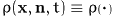 and adopt the following convention:
and adopt the following convention:
- Fields on the nematic space are called mesoscopic
fields
to distinguish them from the "macroscopic" fields defined on the
space of spatial coordinates.
- In formulas this distinction is made by the argument of the
fields: The set of mesoscopic variables is abbreviated as
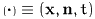 whereas we shall use the argument
whereas we shall use the argument 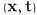 or – if no confusion can arise – no argument
to refer to the macroscopic fields.
or – if no confusion can arise – no argument
to refer to the macroscopic fields.
Since the orientation of a particle is described by a pair of
unit vectors { n, - n} the orientational mass density
is a symmetric (even) function in n.
Then the mass of all particles confined in a spatial volume V having
orientations in the solid angle 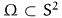 is
is
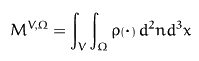
Consequently we have
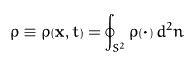
and the local orientational distribution can be specified by the
orientational distribution function (ODF)
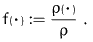
By its very definition f inherits some properties which we
shall keep in mind:
- nematic symmetry: f is even in n.
- positivity: f is non-negative: f>0
- normalization: f can be regarded as a probability
density:
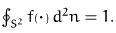
There is a remarkable similarity of our mesoscopic description of
liquid crystals to the theory of mixtures. To emphasize this
connection we compare (note that we introduce the particle number
densities  ):
):
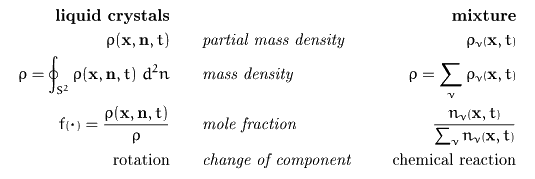
Thus the orientational variable n plays the same role in the
mesoscopic theory as the component index  (up to the difference
that
(up to the difference
that  is a discrete variable with a finite number of possible
values) in the theory of chemical mixtures, and our aim is clearly to
derive the "partial balance equations" for liquid crystals which we
shall call orientational balance equations.
is a discrete variable with a finite number of possible
values) in the theory of chemical mixtures, and our aim is clearly to
derive the "partial balance equations" for liquid crystals which we
shall call orientational balance equations.
A transport theorem and the orientational balance equations
The usual transport theorem of Reynolds can
be extended to  without any difficulties.
without any difficulties.
Proposition 1:Extended Reynolds transport theorem
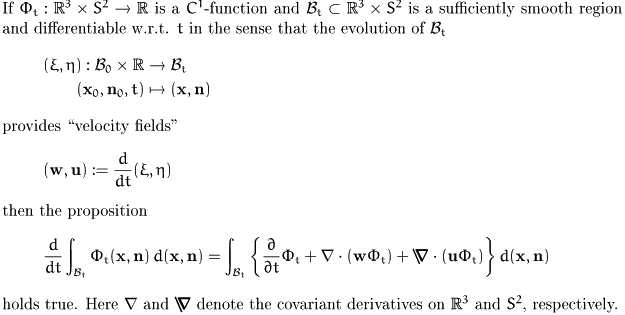
Another proposition which is closely related tells us that there are
no over-all fluxes on the unit sphere:
Proposition 2:
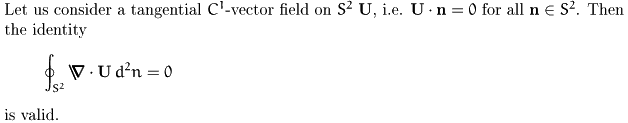
Now we can start considering a body 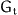 in nematic
space
in nematic
space 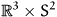 (The following ideas are
strongly influenced by mixture theory and not "quite correct" in a
sense that it is possible to use more strict methods to derive the
same results (see PHYSICA_91).
Since we do not want to complicate matters and the essential ideas
become clear with the simple approach, too, we skip
technical details.) and formulate global balances for particles in a
given spatial region having orientations within a given solid
angle. Since (by the very definition of bodies) the mass in such a
region of the nematic space is conserved we obtain the equation
(The following ideas are
strongly influenced by mixture theory and not "quite correct" in a
sense that it is possible to use more strict methods to derive the
same results (see PHYSICA_91).
Since we do not want to complicate matters and the essential ideas
become clear with the simple approach, too, we skip
technical details.) and formulate global balances for particles in a
given spatial region having orientations within a given solid
angle. Since (by the very definition of bodies) the mass in such a
region of the nematic space is conserved we obtain the equation
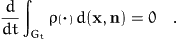
Using the extended Reynolds theorem we conclude that
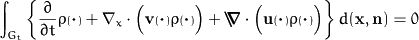
holds true for all regions  , and
, and  and
and
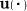 are the material
velocities in the nematic
space. Hence we obtain by continuity the
local form of the balance equation, the orientational balance of
mass
are the material
velocities in the nematic
space. Hence we obtain by continuity the
local form of the balance equation, the orientational balance of
mass
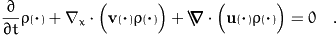
Comparing this equation with the partial mass balance for a single
component of a chemical mixture we see that the orientational
flux 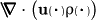 plays
the same role as the source term due to chemical reactions. This
analogy becomes even more true, if we apply proposition 2
and remark that the "net orientational mass production" vanishes
plays
the same role as the source term due to chemical reactions. This
analogy becomes even more true, if we apply proposition 2
and remark that the "net orientational mass production" vanishes
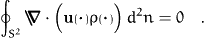
Now we see a general principle: We can formulate the balance equations
we are interested in on the nematic space in the same manner as we did
for the global balances for certain components of a mixture. However,
the "production terms" due to orientational changes are already
accounted for by the extended Reynolds theorem and the concept of
bodies in the nematic space, and we only have to concentrate on the
supplies. Thus the general structure of orientational balance
equations reads
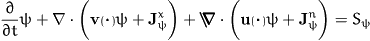
with 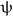 denoting the balanced
quantity,
denoting the balanced
quantity, 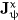 and
and
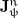 denoting the conductive
(non-convective) fluxes of
denoting the conductive
(non-convective) fluxes of
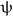 with respect to spatial and
orientational changes, resp., and
with respect to spatial and
orientational changes, resp., and
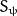 is the supply rate of
is the supply rate of
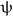 . Thus we obtain the orientational
balances in the form listed below (see also
PHYSICA 91,
MCLC 91,
Liquid Crystals 91):
. Thus we obtain the orientational
balances in the form listed below (see also
PHYSICA 91,
MCLC 91,
Liquid Crystals 91):
- mass:
-
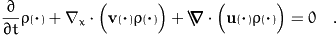
- momentum:
-
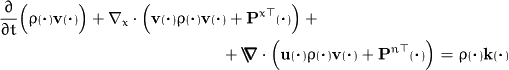
- angular momentum:
-
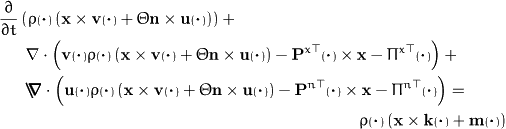
- energy:
-
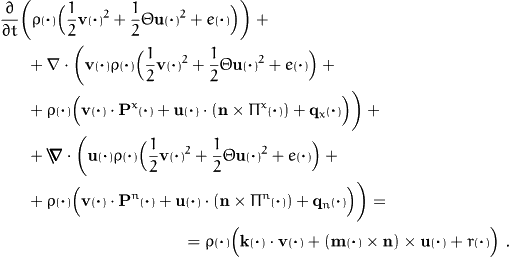
The new quantities are the pressure tensors
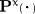 and
and
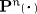 , the couple stress
tensors
, the couple stress
tensors 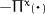 and
and
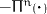 , the heat fluxes
, the heat fluxes
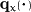 and
and 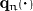 – all of them appearing in
"doublets" concerning spatial and orientational fluxes, resp., – and different supplies as
the force density
– all of them appearing in
"doublets" concerning spatial and orientational fluxes, resp., – and different supplies as
the force density 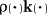 , the torque
density
, the torque
density 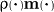 and the radiation
absorption
and the radiation
absorption 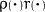 .
.
Macroscopic balance equations
The balances in the previous section are formulated on the nematic
space. For physical applications, however, we need the balances on
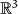 . To obtain them we simply integrate
over all possible
orientations which results in new balance equations and new definitions
of constitutive fields. For this purpose we remember
proposition 2 which tells us that the terms with
. To obtain them we simply integrate
over all possible
orientations which results in new balance equations and new definitions
of constitutive fields. For this purpose we remember
proposition 2 which tells us that the terms with
 do not contribute to the macroscopic
balances.
The resulting equations are those of a micro-polar medium with the
wanted fields
do not contribute to the macroscopic
balances.
The resulting equations are those of a micro-polar medium with the
wanted fields  , v and
s obtained as averages of their mesoscopic counterparts
, v and
s obtained as averages of their mesoscopic counterparts
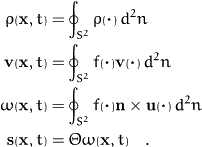
Then the macroscopic balance equations are:
- mass
-
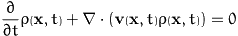
- momentum:
-
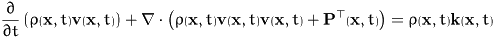
- angular momentum:
-
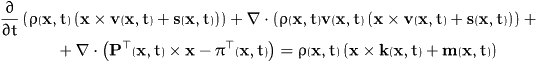
- energy:
-
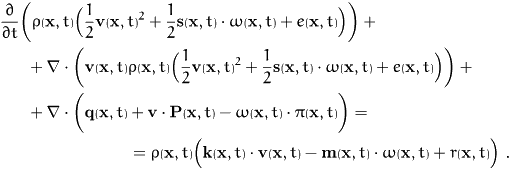
These equations contain new fields which are – of course – obtained
from the mesoscopic fields. In detail we have for the force density
and the pressure tensor
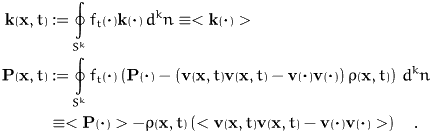
These definitions are supplemented by
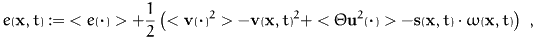
and for the heat flux density and energy supply
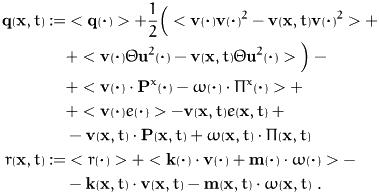
We remark that the pressure tensor is in general not the
average of the mesoscopic pressure tensor but contains additional
kinetic contributions due to the peculiar velocities 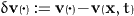 . These terms dominate in the
kinetic theory of gases. Here, however, experiments and computer
simulations show that the kinetic part of the pressure tensor in a
liquid is often negligible in comparison to the potential part. Thus we
shall assume in the following that they can be cancelled (compare
especially the section on
constitutive equations).
Another remark is due
about the spin s. Taking into account the balances of mass
and momentum the redundant parts in the balance of angular momentum
can be removed
and we end up with the spin balance
. These terms dominate in the
kinetic theory of gases. Here, however, experiments and computer
simulations show that the kinetic part of the pressure tensor in a
liquid is often negligible in comparison to the potential part. Thus we
shall assume in the following that they can be cancelled (compare
especially the section on
constitutive equations).
Another remark is due
about the spin s. Taking into account the balances of mass
and momentum the redundant parts in the balance of angular momentum
can be removed
and we end up with the spin balance
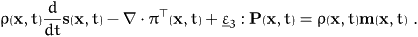
The involved fields s,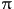 and
m do
not appear in simple continuum models without internal degrees of
freedom. Thus the spin balance results in a proposition about the
symmetry of the pressure tensor:
and
m do
not appear in simple continuum models without internal degrees of
freedom. Thus the spin balance results in a proposition about the
symmetry of the pressure tensor: 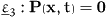 ,
i.e. the pressure tensor is a symmetric tensor.
I addition to the balance equations there is the second
law in the
form of the dissipation
inequality and we can use the methods of Coleman and
Noll or Liu to obtain
restrictions for the constitutive equations. A typical state space
for liquid crystals, however, must contain some quantities describing
the orientational order in the fluid. Since we introduced
orientational fields up to now on the nematic space only and the
validity of the dissipation inequality is restricted to
,
i.e. the pressure tensor is a symmetric tensor.
I addition to the balance equations there is the second
law in the
form of the dissipation
inequality and we can use the methods of Coleman and
Noll or Liu to obtain
restrictions for the constitutive equations. A typical state space
for liquid crystals, however, must contain some quantities describing
the orientational order in the fluid. Since we introduced
orientational fields up to now on the nematic space only and the
validity of the dissipation inequality is restricted to 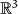 there
is some discrepancy. Thus it is natural to look for macroscopic fields
(i.e. fields on space-time) specifying the orientational distribution
in a volume element of our material.
there
is some discrepancy. Thus it is natural to look for macroscopic fields
(i.e. fields on space-time) specifying the orientational distribution
in a volume element of our material.
Order parameters: The alignment tensor family
The orientational distribution of molecules defines the orientational
distribution function f. If we want to
derive a set of
macroscopic fields which shall represent f on 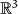 , it is a good idea
to remember the multi-pole expansion of electrostatics where the
electrostatic potential
, it is a good idea
to remember the multi-pole expansion of electrostatics where the
electrostatic potential 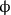 can be
described by the moments of
can be
described by the moments of 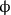 (the
same situation we find in the kinetic theory of
gases). Thus we would like to have a suitable basis on the
orientational part of the domain of f and use the "Fourier
coefficients" with respect to that basis (which are now
macroscopic fields!) to represent f on
(the
same situation we find in the kinetic theory of
gases). Thus we would like to have a suitable basis on the
orientational part of the domain of f and use the "Fourier
coefficients" with respect to that basis (which are now
macroscopic fields!) to represent f on 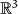 .
This can be done using the following
.
This can be done using the following
Proposition 3:
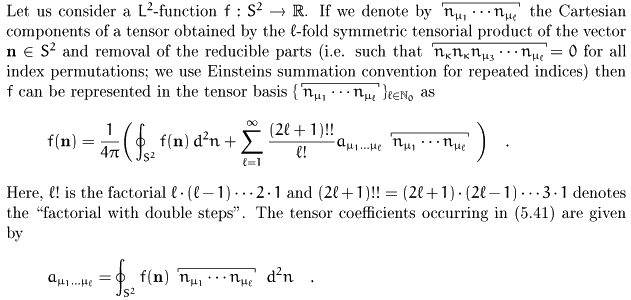
For our purposes the distribution function f is even in
n and its coefficients 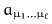 of odd order
vanish. We call the tensor coefficients
of odd order
vanish. We call the tensor coefficients 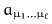 of
f the alignment tensors of f. They are the wanted
macroscopic order parameters which can be
included in the state
space. Nevertheless, there is an infinite number of alignment tensors
and we have to choose how many we want to take into account. Fortunately, the
situations in which we are forced to use more than the first two
alignment tensors (i.e. the second and fourth order tensor) are very rare.
We shall see also that the tensors themselves can have a very special
form in many relevant cases which simplifies the description.
Before we continue a remark on the "quality" of our new fields is in
order: Some variables of
a chosen state space might not be directly controllable (the
so-called internal variables) but
fulfill special evolution
equations. This is true in particular for the alignment tensors. From
the orientational mass balance and the
definition of the orientation distribution function
we obtain a relaxation
equation for f (see
PHYSICA 91) for
f
of
f the alignment tensors of f. They are the wanted
macroscopic order parameters which can be
included in the state
space. Nevertheless, there is an infinite number of alignment tensors
and we have to choose how many we want to take into account. Fortunately, the
situations in which we are forced to use more than the first two
alignment tensors (i.e. the second and fourth order tensor) are very rare.
We shall see also that the tensors themselves can have a very special
form in many relevant cases which simplifies the description.
Before we continue a remark on the "quality" of our new fields is in
order: Some variables of
a chosen state space might not be directly controllable (the
so-called internal variables) but
fulfill special evolution
equations. This is true in particular for the alignment tensors. From
the orientational mass balance and the
definition of the orientation distribution function
we obtain a relaxation
equation for f (see
PHYSICA 91) for
f
Since the alignment tensors are just the multi-pole moments of f it
becomes clear that there are also relaxation equations for
them. Thus the alignment tensors cannot be directly controlled but
have to be considered as internal variables.
In most cases in physics of nematic liquid crystals the
orientation distribution function f possesses a symmetry
axis such that

holds true. The vector d is called the macroscopic
director of the distribution; this case is usually
referred to as uniaxial symmetry
(which must not be confused with the uniaxial symmetry of single
particles – here the symmetry is
due to the distribution of the particles). In this case the
alignment tensors take on a
rather simple form
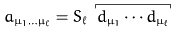
with
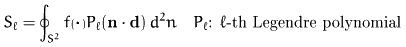 .
.
The most important case of the alignment tensor of second order is
then written as
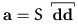
and the scalar order parameter S is
referred to as Maier-Saupe order parameter.
We close this paragraph with the relaxation
equations for the
alignment tensors:
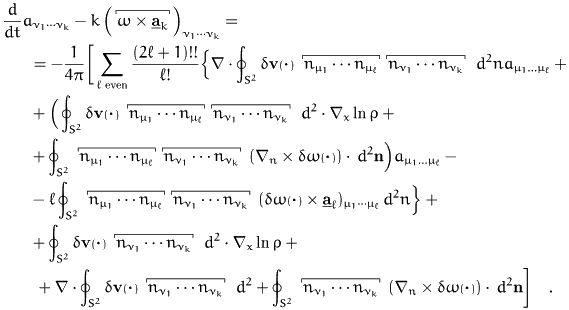
The left hand side of this equation is Jaumann's time
derivative of a symmetric, l-th order tensor. The right hand side
contains terms with the peculiar velocities (translation and rotation).
Thus we can write for short
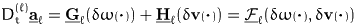
with the alignment production density 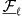 . It is
obvious that
. It is
obvious that
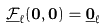
i.e. for a rigid body rotation of the ODF (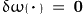 )
and common movement of all particles (
)
and common movement of all particles (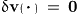 ) there is no alignment production. The essential
problem connected with the alignment tensor balance is that the
differential equation for the l-th alignment tensor cannot be
solved separately from those of the other alignment tensors which
yields a very complicated scheme of equations. For practical purposes
one has to cut down the system and to choose special approximations.
We used two levels to deal with liquid crystals. First, the balances
were formulated on the nematic space (mesoscopic level). Second, the
dissipation inequality and the "measured" fields are fields on
) there is no alignment production. The essential
problem connected with the alignment tensor balance is that the
differential equation for the l-th alignment tensor cannot be
solved separately from those of the other alignment tensors which
yields a very complicated scheme of equations. For practical purposes
one has to cut down the system and to choose special approximations.
We used two levels to deal with liquid crystals. First, the balances
were formulated on the nematic space (mesoscopic level). Second, the
dissipation inequality and the "measured" fields are fields on
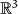 (macroscopic level). Hence we can
formulate constitutive equations with mesoscopic or macroscopic
state spaces.
In some cases
it is even advisable to use a mixed description and include mesoscopic
as well as macroscopic fields in the state space. We shall give two
examples to elucidate the method.
(macroscopic level). Hence we can
formulate constitutive equations with mesoscopic or macroscopic
state spaces.
In some cases
it is even advisable to use a mixed description and include mesoscopic
as well as macroscopic fields in the state space. We shall give two
examples to elucidate the method.
Macroscopic constitutive theory, exploitation of the
dissipation inequality
We saw already that a liquid crystal theory should contain some
macroscopic order parameter. In its most simple
form this is the (macroscopic) director d (for
situations with uniaxial symmetry and nearly perfect order of the
molecules) or in more
complicated and general cases some alignment tensors. The inclusion of
d alone, however, is not enough since a liquid crystal can be
distorted and the elastic energy due to that
distortion can not be neglected (see Fig. 3).

Figure 3: Elastic distortions of a nematic liquid
crystal: (a) splay (b) twist (c) bend
The elastic part of the free energy due to these distortions is
expressed by d
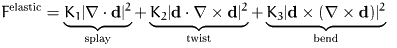 .
.
Thus the state space must contain gradients of the macroscopic order
parameters in addition to the order parameters themselves. A typical
state space reads as follows:
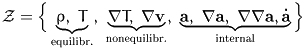 .
.
It is easy to imagine that an exploitation of the dissipation
inequality for such a state space is a tedious enterprise. The length
of the calculations is even for the simpler method of Coleman and
Noll surprising (nothing to say about the Liu procedure) but gives some
interesting insight in the constitutive theory of liquid crystals. We
cannot perform the calculations here, but present only some results
(see e.g.
Int. J. Engng. Sci. 92,
Liquid Crystals
93)
which appear in the form "that something does not depend on something
else":
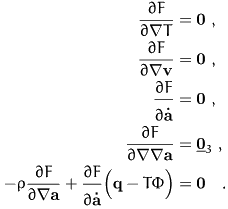
Thus the free energy F would be independent on 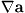 if the excess heat flux
if the excess heat flux 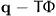 (
(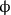 is
the entropy flux density) vanishes – which clearly is
impossible as we saw above. Hence liquid crystals are one example
where heat flux density and entropy flux density have a more involved
connection as it is presupposed in the thermodynamics irreversible
processes (TIP). This is not surprising: entropy transfer in
a liquid crystal can be observed without heat conduction since
reorientation of the molecules clearly affects the entropy, but is not
necessarily connected with a temperature gradient.
The restrictions imposed by the second law, however, are rather weak
and do not yield specific expressions for the constitutive
quantities. We shall study an explicit example in the next paragraph.
is
the entropy flux density) vanishes – which clearly is
impossible as we saw above. Hence liquid crystals are one example
where heat flux density and entropy flux density have a more involved
connection as it is presupposed in the thermodynamics irreversible
processes (TIP). This is not surprising: entropy transfer in
a liquid crystal can be observed without heat conduction since
reorientation of the molecules clearly affects the entropy, but is not
necessarily connected with a temperature gradient.
The restrictions imposed by the second law, however, are rather weak
and do not yield specific expressions for the constitutive
quantities. We shall study an explicit example in the next paragraph.
Mesoscopic constitutive theory, viscosity of a nematic liquid
crystal
We want to describe the viscous behaviour of a nematic liquid
crystal. For this purpose we choose a mesoscopic state space
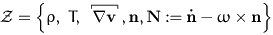
with 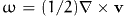 denoting the
vorticity of the flow field. N is then the so-called
co-rotational time derivative of the microscopic director
n. This state space is sufficient to deal with viscous
properties of an anisotropic fluid. If we restrict our attention to an
ansatz for the pressure tensor which contains no quadratic or higher
terms in the shear rate tensor
denoting the
vorticity of the flow field. N is then the so-called
co-rotational time derivative of the microscopic director
n. This state space is sufficient to deal with viscous
properties of an anisotropic fluid. If we restrict our attention to an
ansatz for the pressure tensor which contains no quadratic or higher
terms in the shear rate tensor 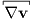 , it
is rather
easy to write down a representation theorem for
the pressure tensor. Before we do that we split the pressure tensor in its
equilibrium part and the friction pressure tensor
, it
is rather
easy to write down a representation theorem for
the pressure tensor. Before we do that we split the pressure tensor in its
equilibrium part and the friction pressure tensor
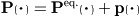
where the dependence on 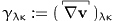 is contained only in
p. Now the ansatz for p is due to
Leslie (who used it for the macroscopic director)
and reads
is contained only in
p. Now the ansatz for p is due to
Leslie (who used it for the macroscopic director)
and reads
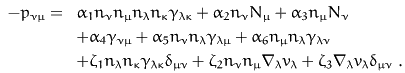
The coefficients are usually referred to as Leslie
coefficients. From our previous considerations we know that for
negligible peculiar velocities 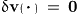 the
pressure tensor on
the
pressure tensor on  is the
average (integration with f over all orientations) of the
mesoscopic pressure tensor. Thus we write
is the
average (integration with f over all orientations) of the
mesoscopic pressure tensor. Thus we write

For uniaxial distribution functions the occurring averages can be
explicitly calculated and we end up with an expression for the friction
pressure tensor which involves the Leslie coefficients and the scalar
order parameters 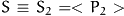 and
and 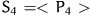 (see
Phys. Rev. 95).
(see
Phys. Rev. 95).
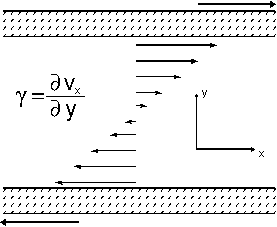
Figure 4: Geometry of a plane Couette flow (simple shear flow)
Considering a plane Couette flow (compare Fig. 4) we can
distinguish 3 different cases: If we apply a magnetic field (which is
capable of aligning the mean orientation, i.e. the macroscopic
director, of the liquid crystal) the
resistance of the fluid to the movement of the plates depends on the
orientation of the director with respect to the flow. The highest
viscosity is obtained for d parallel to the gradient
direction (y-direction in Fig. 4), whereas alignment parallel to the
flow direction (z-direction in Fig. 4) yields the lowest
viscosity. These viscosities with fixed director aligned parallel to
the three main axes of the flow are usually referred
to as Miesowicz viscosities.
Fig. 5 shows the theoretical prediction
for a system of ellipsoidal particles. The theoretical curves are
compared with measured data for some members of the family of
cyanobiphenyls. The free parameter of the model is the axis ratio of
the ellipsoidal particles.
Figure 5: Miesowicz viscosities of some cyanobiphenyls
Use the mouse (left button to change the apect
ratio, right button - or left button together with meta key (ESCAPE on
most systems) - to shift) to adjust the "ellipsoid" enclosing
the space filling model and watch the theoretical curves fitting the
measured data!
A survey on anisotropic fluids is certainly incomplete, if the famous
application of liquid crystals in display technology is not
mentioned. Therefore we shall describe the twisted
nematic (TN) cell which is the simplest type of display,
cheap and widely used in many applications. The principle idea is
simple: The mean orientation of a nematic liquid crystal is influenced
by the boundary conditions and external (electric) fields. If we
manage to combine these two orienting sources in such a way that we
can switch the orientation by applying the electric field, we have
changed the optical properties of the fluid. Use of polarization
filters might produce a device with two states: dark and bright,
according to the state of the electric field.
The general physical setup is sketched in Fig. 6.
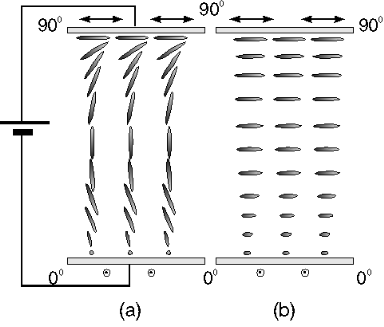
Figure 6: A liquid crystal is inserted between two crossed, orienting
layers yielding a twist of the director field (b). The molecules
reorient under the influence of an applied electric field
(a).
Two plates are prepared in such a way (this can be done, e.g,
by rubbing the surface of the plates in one direction) that the
molecules align in a certain direction at the surface. Thus it is
possible to prescribe a mean orientation in the cell by the
arrangement of the two plates . If we ensure
that the plates are crossed, the induced director field resembles a
helical structure (see (b) in Fig. 6) which gives
rise to the name twisted nematic cell. The plane of
polarization of the incoming light is guided according to the local orientation
of the liquid crystal ("wave guiding"), and performs therefore a
rotation of 90° passing the cell. If we apply an electric field
(see (a) in Fig. 6), the liquid crystal is forced
to align along the field direction. In this configuration there is no
(or hardly none) optical anisotropy for the passing light beam, and
the polarization plane does not change. Thus we can switch between two
states with different polarizations of the passing (or reflected)
beam. We complete this setup by two polarizers and obtain a display
which can switch from
a dark to a bright state. This is the principle of most
liquid crystal displays.
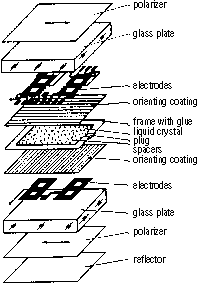
Figure 7: Structure of a TN (twisted nematic) cell
Some final remarks
The survey on liquid crystals was very brief. Nevertheless, we saw
some essential principles at work:
- The internal structure of the medium gives rise to additional
fields. Those fields can be introduced from a background theory
which deals with adjusted configuration spaces and induces the order
parameters. Note that the notion of order
parameters is quite general
and not restricted to the sense we gave the word in our
context. Other applications can be found in many other areas
(e.g. Landau theory of phase transitions, superconductivity, and
more).
- In many cases there will be a set of additional equations for the
new fields which govern their evolution and prohibit the direct
access from the "outside". Thus the general context is
a thermodynamical theory with internal
variables.
- According to the structure of the model constitutive equations
can be formulated both on the macroscopic level as well as on finer
levels of a an adapted configuration space. The second
law, however,
can only be used on the macroscopic niveau. Nevertheless, a finer
background can be used to obtain structural information on constitutive
quantities which supplement the restrictions originating from the
dissipation inequality.
Thus the phenomenological concepts of thermodynamics can be used in
the theory of liquid crystals even out of the situations they were
originally designed for. Liquid crystals are only an example we used here
to demonstrate (at least) some of the methods used in modern constitutive
theory.
Harald Ehrentraut
Institut für Theoretische Physik
TU Berlin, March 6th 1997
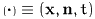 whereas we shall use the argument
whereas we shall use the argument 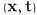 or – if no confusion can arise – no argument
to refer to the macroscopic fields.
or – if no confusion can arise – no argument
to refer to the macroscopic fields.


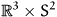 . On this space we introduce the orientational mass
density
. On this space we introduce the orientational mass
density
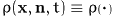 and adopt the following convention:
and adopt the following convention:
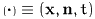 whereas we shall use the argument
whereas we shall use the argument 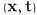 or – if no confusion can arise – no argument
to refer to the macroscopic fields.
or – if no confusion can arise – no argument
to refer to the macroscopic fields.
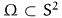 is
is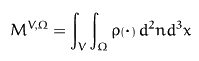
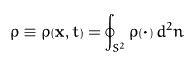
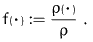
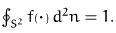
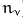 ):
):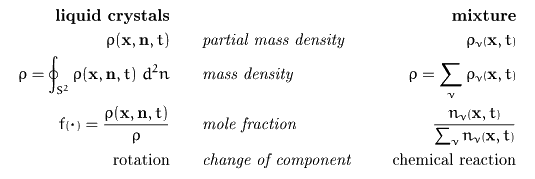
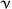 (up to the difference
that
(up to the difference
that 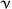 is a discrete variable with a finite number of possible
values) in the theory of chemical mixtures, and our aim is clearly to
derive the "partial balance equations" for liquid crystals which we
shall call orientational balance equations.
is a discrete variable with a finite number of possible
values) in the theory of chemical mixtures, and our aim is clearly to
derive the "partial balance equations" for liquid crystals which we
shall call orientational balance equations.
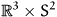 without any difficulties.
without any difficulties.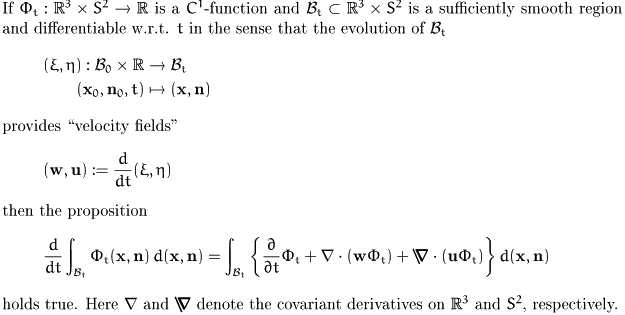
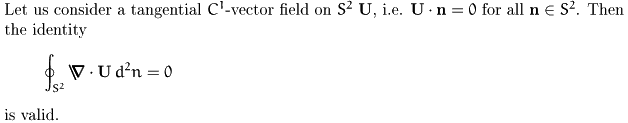
 in nematic
space
in nematic
space 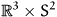 (The following ideas are
strongly influenced by mixture theory and not "quite correct" in a
sense that it is possible to use more strict methods to derive the
same results (see PHYSICA_91).
Since we do not want to complicate matters and the essential ideas
become clear with the simple approach, too, we skip
technical details.) and formulate global balances for particles in a
given spatial region having orientations within a given solid
angle. Since (by the very definition of bodies) the mass in such a
region of the nematic space is conserved we obtain the equation
(The following ideas are
strongly influenced by mixture theory and not "quite correct" in a
sense that it is possible to use more strict methods to derive the
same results (see PHYSICA_91).
Since we do not want to complicate matters and the essential ideas
become clear with the simple approach, too, we skip
technical details.) and formulate global balances for particles in a
given spatial region having orientations within a given solid
angle. Since (by the very definition of bodies) the mass in such a
region of the nematic space is conserved we obtain the equation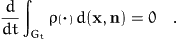
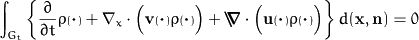
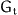 , and
, and 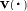 and
and
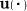 are the material
velocities in the nematic
space. Hence we obtain by continuity the
local form of the balance equation, the orientational balance of
mass
are the material
velocities in the nematic
space. Hence we obtain by continuity the
local form of the balance equation, the orientational balance of
mass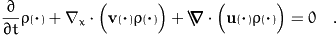
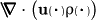 plays
the same role as the source term due to chemical reactions. This
analogy becomes even more true, if we apply proposition 2
and remark that the "net orientational mass production" vanishes
plays
the same role as the source term due to chemical reactions. This
analogy becomes even more true, if we apply proposition 2
and remark that the "net orientational mass production" vanishes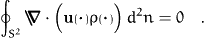
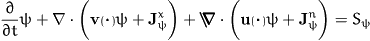
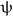 denoting the balanced
quantity,
denoting the balanced
quantity, 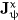 and
and
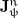 denoting the conductive
(non-convective) fluxes of
denoting the conductive
(non-convective) fluxes of
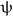 with respect to spatial and
orientational changes, resp., and
with respect to spatial and
orientational changes, resp., and
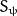 is the supply rate of
is the supply rate of
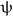 . Thus we obtain the orientational
balances in the form listed below (see also
PHYSICA 91,
MCLC 91,
Liquid Crystals 91):
. Thus we obtain the orientational
balances in the form listed below (see also
PHYSICA 91,
MCLC 91,
Liquid Crystals 91):
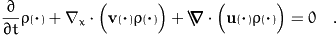
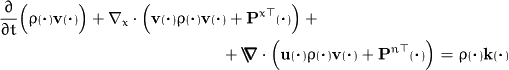
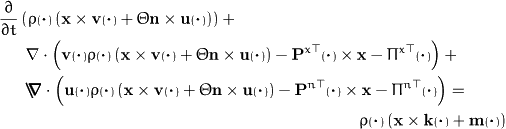
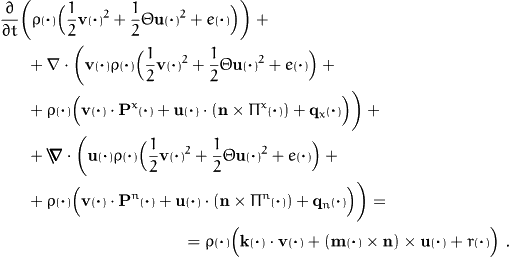
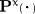 and
and
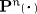 , the couple stress
tensors
, the couple stress
tensors 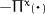 and
and
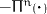 , the heat fluxes
, the heat fluxes
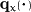 and
and 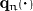 – all of them appearing in
"doublets" concerning spatial and orientational fluxes, resp., – and different supplies as
the force density
– all of them appearing in
"doublets" concerning spatial and orientational fluxes, resp., – and different supplies as
the force density 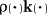 , the torque
density
, the torque
density 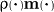 and the radiation
absorption
and the radiation
absorption 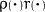 .
.
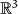 . To obtain them we simply integrate
over all possible
orientations which results in new balance equations and new definitions
of constitutive fields. For this purpose we remember
proposition 2 which tells us that the terms with
. To obtain them we simply integrate
over all possible
orientations which results in new balance equations and new definitions
of constitutive fields. For this purpose we remember
proposition 2 which tells us that the terms with
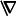 do not contribute to the macroscopic
balances.
The resulting equations are those of a micro-polar medium with the
wanted fields
do not contribute to the macroscopic
balances.
The resulting equations are those of a micro-polar medium with the
wanted fields 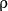 ,
, 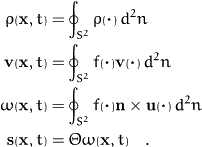
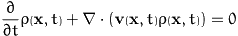
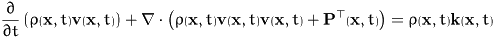
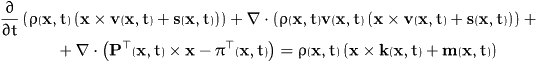
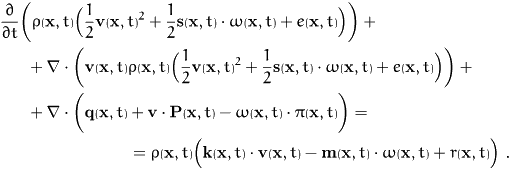
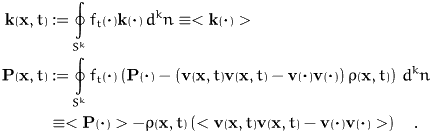
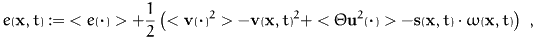
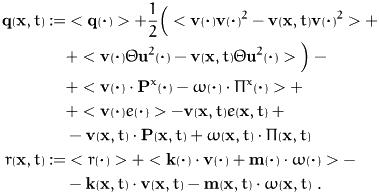
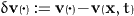 . These terms dominate in the
kinetic theory of gases. Here, however, experiments and computer
simulations show that the kinetic part of the pressure tensor in a
liquid is often negligible in comparison to the potential part. Thus we
shall assume in the following that they can be cancelled (compare
especially the section on
constitutive equations).
Another remark is due
about the spin
. These terms dominate in the
kinetic theory of gases. Here, however, experiments and computer
simulations show that the kinetic part of the pressure tensor in a
liquid is often negligible in comparison to the potential part. Thus we
shall assume in the following that they can be cancelled (compare
especially the section on
constitutive equations).
Another remark is due
about the spin 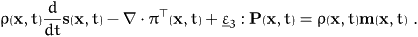
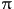 and
and
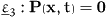 ,
i.e. the pressure tensor is a symmetric tensor.
I addition to the balance equations there is the second
law in the
form of the dissipation
inequality and we can use the methods of Coleman and
Noll or Liu to obtain
restrictions for the constitutive equations. A typical state space
for liquid crystals, however, must contain some quantities describing
the orientational order in the fluid. Since we introduced
orientational fields up to now on the nematic space only and the
validity of the dissipation inequality is restricted to
,
i.e. the pressure tensor is a symmetric tensor.
I addition to the balance equations there is the second
law in the
form of the dissipation
inequality and we can use the methods of Coleman and
Noll or Liu to obtain
restrictions for the constitutive equations. A typical state space
for liquid crystals, however, must contain some quantities describing
the orientational order in the fluid. Since we introduced
orientational fields up to now on the nematic space only and the
validity of the dissipation inequality is restricted to 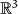 there
is some discrepancy. Thus it is natural to look for macroscopic fields
(i.e. fields on space-time) specifying the orientational distribution
in a volume element of our material.
there
is some discrepancy. Thus it is natural to look for macroscopic fields
(i.e. fields on space-time) specifying the orientational distribution
in a volume element of our material.
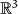 , it is a good idea
to remember the multi-pole expansion of electrostatics where the
electrostatic potential
, it is a good idea
to remember the multi-pole expansion of electrostatics where the
electrostatic potential 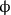 can be
described by the moments of
can be
described by the moments of 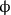 (the
same situation we find in the kinetic theory of
gases). Thus we would like to have a suitable basis on the
orientational part of the domain of f and use the "Fourier
coefficients" with respect to that basis (which are now
macroscopic fields!) to represent f on
(the
same situation we find in the kinetic theory of
gases). Thus we would like to have a suitable basis on the
orientational part of the domain of f and use the "Fourier
coefficients" with respect to that basis (which are now
macroscopic fields!) to represent f on  .
This can be done using the following
.
This can be done using the following 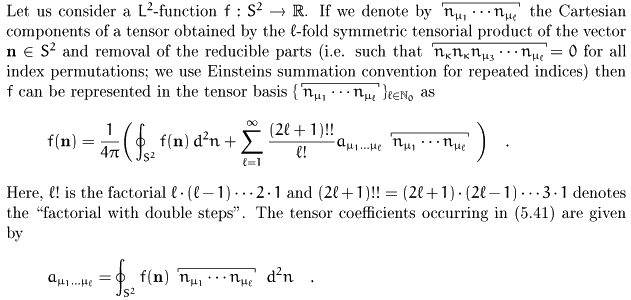
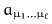 of odd order
vanish. We call the tensor coefficients
of odd order
vanish. We call the tensor coefficients 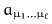 of
f the alignment tensors of f. They are the wanted
macroscopic order parameters which can be
included in the state
space. Nevertheless, there is an infinite number of alignment tensors
and we have to choose how many we want to take into account. Fortunately, the
situations in which we are forced to use more than the first two
alignment tensors (i.e. the second and fourth order tensor) are very rare.
We shall see also that the tensors themselves can have a very special
form in many relevant cases which simplifies the description.
Before we continue a remark on the "quality" of our new fields is in
order: Some variables of
a chosen state space might not be directly controllable (the
so-called internal variables) but
fulfill special evolution
equations. This is true in particular for the alignment tensors. From
the orientational mass balance and the
definition of the orientation distribution function
we obtain a relaxation
equation for f (see
PHYSICA 91) for
f
of
f the alignment tensors of f. They are the wanted
macroscopic order parameters which can be
included in the state
space. Nevertheless, there is an infinite number of alignment tensors
and we have to choose how many we want to take into account. Fortunately, the
situations in which we are forced to use more than the first two
alignment tensors (i.e. the second and fourth order tensor) are very rare.
We shall see also that the tensors themselves can have a very special
form in many relevant cases which simplifies the description.
Before we continue a remark on the "quality" of our new fields is in
order: Some variables of
a chosen state space might not be directly controllable (the
so-called internal variables) but
fulfill special evolution
equations. This is true in particular for the alignment tensors. From
the orientational mass balance and the
definition of the orientation distribution function
we obtain a relaxation
equation for f (see
PHYSICA 91) for
f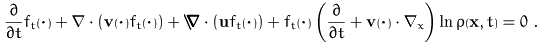

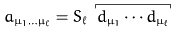
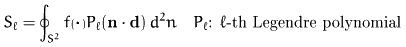 .
.
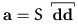
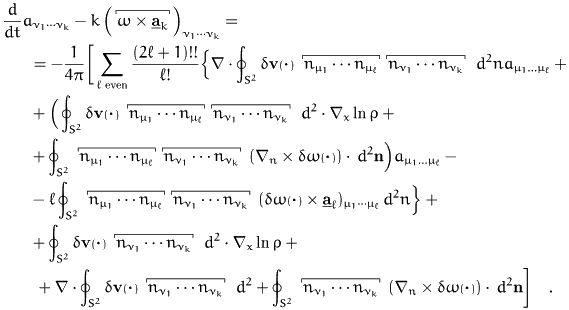
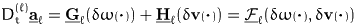
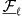 . It is
obvious that
. It is
obvious that 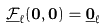
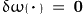 )
and common movement of all particles (
)
and common movement of all particles (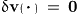 ) there is no alignment production. The essential
problem connected with the alignment tensor balance is that the
differential equation for the l-th alignment tensor cannot be
solved separately from those of the other alignment tensors which
yields a very complicated scheme of equations. For practical purposes
one has to cut down the system and to choose special approximations.
) there is no alignment production. The essential
problem connected with the alignment tensor balance is that the
differential equation for the l-th alignment tensor cannot be
solved separately from those of the other alignment tensors which
yields a very complicated scheme of equations. For practical purposes
one has to cut down the system and to choose special approximations.
 (macroscopic level). Hence we can
formulate constitutive equations with mesoscopic or macroscopic
state spaces.
In some cases
it is even advisable to use a mixed description and include mesoscopic
as well as macroscopic fields in the state space. We shall give two
examples to elucidate the method.
(macroscopic level). Hence we can
formulate constitutive equations with mesoscopic or macroscopic
state spaces.
In some cases
it is even advisable to use a mixed description and include mesoscopic
as well as macroscopic fields in the state space. We shall give two
examples to elucidate the method.

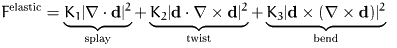 .
.
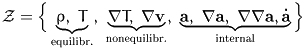 .
.
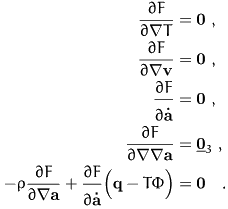
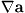 if the excess heat flux
if the excess heat flux 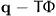 (
(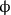 is
the entropy flux density) vanishes – which clearly is
impossible as we saw above. Hence liquid crystals are one example
where heat flux density and entropy flux density have a more involved
connection as it is presupposed in the thermodynamics irreversible
processes (TIP). This is not surprising: entropy transfer in
a liquid crystal can be observed without heat conduction since
reorientation of the molecules clearly affects the entropy, but is not
necessarily connected with a temperature gradient.
The restrictions imposed by the second law, however, are rather weak
and do not yield specific expressions for the constitutive
quantities. We shall study an explicit example in the next paragraph.
is
the entropy flux density) vanishes – which clearly is
impossible as we saw above. Hence liquid crystals are one example
where heat flux density and entropy flux density have a more involved
connection as it is presupposed in the thermodynamics irreversible
processes (TIP). This is not surprising: entropy transfer in
a liquid crystal can be observed without heat conduction since
reorientation of the molecules clearly affects the entropy, but is not
necessarily connected with a temperature gradient.
The restrictions imposed by the second law, however, are rather weak
and do not yield specific expressions for the constitutive
quantities. We shall study an explicit example in the next paragraph.
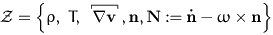
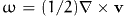 denoting the
vorticity of the flow field.
denoting the
vorticity of the flow field. 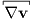 , it
is rather
easy to write down a representation theorem for
the pressure tensor. Before we do that we split the pressure tensor in its
equilibrium part and the friction pressure tensor
, it
is rather
easy to write down a representation theorem for
the pressure tensor. Before we do that we split the pressure tensor in its
equilibrium part and the friction pressure tensor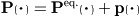
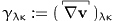 is contained only in
is contained only in
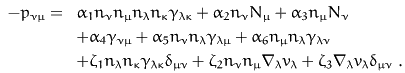
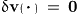 the
pressure tensor on
the
pressure tensor on 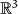 is the
average (integration with f over all orientations) of the
mesoscopic pressure tensor. Thus we write
is the
average (integration with f over all orientations) of the
mesoscopic pressure tensor. Thus we write 
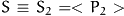 and
and 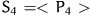 (see
Phys. Rev. 95).
(see
Phys. Rev. 95).


