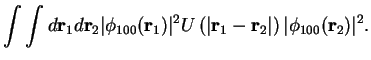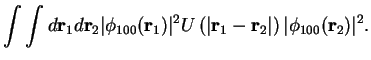Next: Excited states
Up: Perturbation theory in
Previous: Perturbation theory in
Contents
Index
The unperturbed ground state has
 and
and
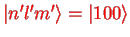 , i.e.
, i.e.
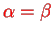 with a symmetrical orbital wave function
with a symmetrical orbital wave function
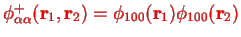 and a singlet spinor
and a singlet spinor
 . The energy to first order in
. The energy to first order in
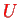 therefore is
therefore is
Calculation of
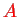 yields
yields
For
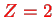 , one has
, one has
 eV and
eV and
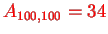 eV such that
eV such that
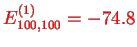 eV.
eV.
Exercise: Calculate the integral leading to the result Eq. (III.3.5). Solution hints are given in Gasiorowicz [3].
Tobias Brandes
2005-04-26