




Next: - Representation
Up: Derivation of Master equation
Previous: Derivation of Master equation
Contents
Index
We note that
 .
In the secular approximation, one sets
.
In the secular approximation, one sets
The real parts of
 and
and
 are zero because
are zero because
 yields no contribution from the integral (remember that
yields no contribution from the integral (remember that
 ). This approximation therefore
neglects the imaginary parts of
). This approximation therefore
neglects the imaginary parts of
 and
and
 which, however,
do not lead to damping but only to a renormalisation of the system Hamiltonian
which, however,
do not lead to damping but only to a renormalisation of the system Hamiltonian 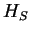 .
For consistency, we therefore neglect the imaginary parts of
.
For consistency, we therefore neglect the imaginary parts of
 and
and
 as well.
Therefore,
as well.
Therefore,





Next: - Representation
Up: Derivation of Master equation
Previous: Derivation of Master equation
Contents
Index
Tobias Brandes
2004-02-18




![$\displaystyle \frac{1}{2}(\gamma_++\gamma) = \pi\rho(\Omega)[1+2n_B(\omega)]$](img279.png)
