Derivation of Master equation (non-RWA), secular approximation

We now move on to derive the Master equation for the non-RWA model. Using $\tilde{S}(t)=ae^{-i\Omega t} +a^{\dagger}e^{i\Omega t}$, we have

$$D \equiv \int_0^{\infty}d \tau C(\tau)\tilde{S}(-\tau)= \int_0^{\infty}d \tau C(\tau) \left[ae^{i\Omega \tau} +a^{\dagger}e^{-i\Omega \tau}\right]$$

$$= \hat{C}(-i\Omega) a + \hat{C}(i\Omega) a^{\dagger}\equiv c_-a + c_+a^{\dagger}$$

$$E \equiv \int_0^{\infty}d \tau C^*(\tau)\tilde{S}(-\tau)= \int_0^{\infty}d \tau C^*(\tau)\tilde{S}^{\dagger}(-\tau)=D^{\dagger}$$

$$= c_+^*a + c_-^*a^{\dagger},$$ (63)

where we used the Laplace transform of $C(\tau)$,

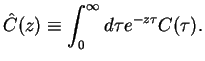$$\hat{C}(z)\equiv \int_{0}^{\infty}d\tau e^{-z\tau} C(\tau).$$ (64)