Next: Master Equation IV: Phase
Up: Derivation of Master equation
Previous: `Secular approximation'
Contents
Index
We now can write
where we again used
 Using
Using
 , one obtains the Master equation from the Non-RWA Model in secular approximation,
, one obtains the Master equation from the Non-RWA Model in secular approximation,
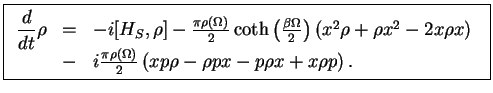 |
|
|
(67) |
Tobias Brandes
2004-02-18