




Next: Rotating Wave Approximation (RWA)
Up: Atom + Electrical Field
Previous: Model Atom
Contents
Index
Consider an electrical field in the form of a linearly polarised, monochromatic plain wave with
wave vector  ,
,
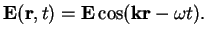 |
|
|
(114) |
Describe the interaction of the atom with the electrical field in dipole approximation: the energy of a
dipole  in a field
in a field
 is given by
is given by
 . Treating the
field classically, we obtain the time-dependent dipole Hamiltonian
. Treating the
field classically, we obtain the time-dependent dipole Hamiltonian
where we used
 in the overlap integral (wave length
in the overlap integral (wave length  dimension of atom, `dipole approximation'), and introduced
dimension of atom, `dipole approximation'), and introduced
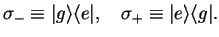 |
|
|
(116) |
and the Rabi frequency
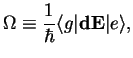 |
|
|
(117) |
which in general is a complex number.
The total system Hamiltonian therefore is
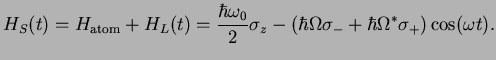 |
|
|
(118) |
One usually assumes real
 , in this case we can formally write
, in this case we can formally write
 with
with
![\begin{displaymath}{\bf B}(t)=\left(
\begin{array}[h]{c}
-\hbar\Omega\cos(\omega t)\\ 0\\ \frac{1}{2}\hbar\omega_0 \end{array} \right).\end{displaymath}](img545.png) |
|
|
(119) |





Next: Rotating Wave Approximation (RWA)
Up: Atom + Electrical Field
Previous: Model Atom
Contents
Index
Tobias Brandes
2004-02-18
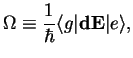
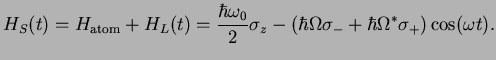
![\begin{displaymath}{\bf B}(t)=\left(
\begin{array}[h]{c}
-\hbar\Omega\cos(\omega t)\\ 0\\ \frac{1}{2}\hbar\omega_0 \end{array} \right).\end{displaymath}](img545.png)