




Next: Landau-Zener-Rosen problem
Up: Spin in Magnetic Field
Previous: Constant
Contents
Index
This is defined as for constant field in
 direction and an oscillating field in the
direction and an oscillating field in the
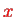 -
-
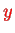 plane,
plane,
 |
|
|
(2.10) |
Our equation for
 thus becomes
thus becomes
This can be solved using the exponential ansatz method
 which yields a quadratic equation for
which yields a quadratic equation for
 ,
,
Note that the term
 in the Rabi-frequency is determined by the level-splitting
in the Rabi-frequency is determined by the level-splitting
 in absence of the time-dependent field
in absence of the time-dependent field
 . The solution for
. The solution for
 (from which
(from which
 follows immediately) therefore is
follows immediately) therefore is
We can choose, e.g., the initial condition
 from which follows
from which follows
This leads to
Note that the quantum-mechanical oscillations at constant
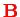 (e.g., the case
(e.g., the case
 in Eq. (VI.1.18)) occur for a time-independent Hamiltonian.
The Rabi-oscillations occur in a time-dependent Hamiltonian containing a time-dependent term (`time-dependent field'). These two often get mixed up in the literature.
in Eq. (VI.1.18)) occur for a time-independent Hamiltonian.
The Rabi-oscillations occur in a time-dependent Hamiltonian containing a time-dependent term (`time-dependent field'). These two often get mixed up in the literature.





Next: Landau-Zener-Rosen problem
Up: Spin in Magnetic Field
Previous: Constant
Contents
Index
Tobias Brandes
2005-04-26
![$\displaystyle i\frac{\dot{B_{\Vert}}}{B_{\Vert}} \dot{\psi}_2 + \left[ \frac{\d...
...}}{B_{\Vert}} B_z
-i B_z^2 -i \vert B_{\Vert}\vert^2 - \dot{B}_z \right] \psi_2$](img1104.png)


![$\displaystyle e^{i\frac{\omega}{2}t}\left[ c'_1 \cos \frac{\Omega_R}{2} t +
c'_2 \sin \frac{\Omega_R}{2} t\right].$](img1121.png)
![$\displaystyle e^{i\frac{\omega}{2}t} \left[\cos \frac{\Omega_R}{2} t
+ c'_2 \sin \frac{\Omega_R}{2} t\right]$](img1123.png)

