Constant ${\bf B}$

In this case we must of course recover our usual two-level system:

$$i \ddot{\psi}_2 = -i[B_z^2+ \vert B_{\Vert}\vert^2] \psi_2 = -i\vert{\bf B}\vert^2 \psi_2$$ (2.6)

$$\leadsto \ddot{\psi}_2 + \vert{\bf B}\vert^2 \psi_2 =$$ 0 (2.7)

$$\leadsto \psi_2(t) = \psi_2(0) \cos \vert{\bf B}\vert t + \frac{\dot{\psi}_2(0)}{\vert{\bf B}\vert} \sin \vert{\bf B}\vert t$$ (2.8)

For constant 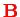${\bf B}$, the eigenvalues of the Hamiltonian

$${\mathcal H} \equiv \left( \begin{matrix}B_z & B_{\Vert}^*\\ B_{\Vert} & - B_z\end{matrix}\right)$$ (2.9)

are given by $(B_z-\varepsilon) (-B_z-\varepsilon) - \vert B_{\Vert}\vert^2= 0$ or $\varepsilon_{\pm} = \pm \sqrt{ B_z^2+ \vert B_{\Vert}\vert^2} = \pm \vert{\bf B}\vert$. Therefore, Eq. (VI.2.6) describes quantum mechanical oscillations with angular frequency of half the level splitting $2\vert{\bf B}\vert$ between ground and excited state, in agreement with our specific example $B_z=0, B_{\Vert}= T_c$ from section VI.1.2.3.