Gauge invariance in single-particle non-relativistic QM

Here, we follow Merzbacher [2].

We now look at the interaction between charges and the electromagnetic field. The first step is to find the Hamiltonian, which is done via the sequence `classical Lagrangian - classical Hamiltonian - QM Hamiltonian'. For a particle of mass $m$ with charge $q$ in an electromagnetic field described by potentials $(\phi, \mathbf{A})$, the classical Hamiltonian is

$${\mathcal H} = H(t) + H_{\rm rad},\quad H(t) \equiv \frac{1}{2m}\left({\bf p}-q \mathbf{A}\right)^2 + q \phi$$ (2.1)

$$H_{\rm rad} = \frac{1}{2}\int d{\bf r} \left[ \varepsilon_0 \mathbf{E}_\perp^2 + \mu_0^{-1} \mathbf{B}^2\right].$$ (2.2)

The em field are still treated classically here. The replacement of the momentum ${\bf p}$ by

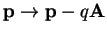$${\bf p} \to {\bf p}-q \mathbf{A}$$ (2.3)

is called minimal coupling. The term $H_{\rm rad}$ is the energy of the electromagnetic field.