Local Gauge Transformation

If we change

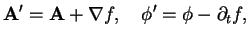$$\mathbf{A}'=\mathbf{A}+ \nabla f,\quad \phi' = \phi -\partial_t f,$$ (2.4)

the Hamiltonian in the new gauge becomes ( $H_{\rm rad}$ is not changed)

$$H'(t) \equiv \frac{1}{2m}\left({\bf p}-q \mathbf{A}' \right)^2 + q \phi'$$ (2.5)

The time-dependent Schrödinger equations in the old and the new gauge are

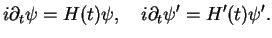$$i\partial_t \psi = H(t)\psi,\quad i\partial_t \psi'= H'(t)\psi'.$$ (2.6)

They should describe the same physics which is the case if

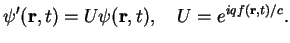$$\psi'({\bf r},t) = U \psi({\bf r},t),\quad U = e^{iqf({\bf r},t)/c}.$$ (2.7)

This can be seen by

$$i\partial_t \psi' = i\partial_t U \psi = (i\partial_t U) \psi+ i U \partial_t\psi = (i\partial_t U) \psi+ i U H\psi = \left[(i\partial_t U) + U H \right] \psi$$

$$= \left[(i\partial_t U) + U H \right]U^{\dagger} U \psi= \left[(i\partial_t U) + U H \right]U^{\dagger} \psi' = H'\psi'$$

$$\leftrightarrow H' = (i\partial_t U) U^{\dagger}+ U H U^{\dagger},$$ (2.8)

which means

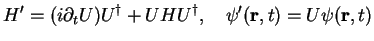$$H' = (i\partial_t U) U^{\dagger}+ U H U^{\dagger},\quad \psi'({\bf r},t) = U \psi({\bf r},t) \leftrightarrow$$    same physics.

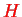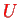The transformation from $H$ to $H'$ and correspondingly $\psi$ to $\psi'$ is completely arbitrary and works for any Hamiltonian and transformation (operator) $U$. In the context we are discussing it here, 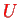$U$ is a phase and thus an element of the group $U(1)$. The transformation $U= e^{iqf({\bf r},t)/c}$ is a local gauge transformation as it involves a ${\bf r}$-dependent phase.