Coulomb Gauge

The Coulomb gauge theory is obtained with the choice

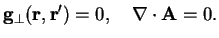$${\bf g}_\perp({\bf r},{\bf r}') =0,\quad \div\mathbf{A}=0.$$ (3.9)

The Hamiltonian in the Coulomb gauge then is

$${\mathcal H}_{\rm Coul} (t) = H(t) + H_{\rm rad}$$

$$H_{\rm rad} = \frac{1}{2}\int d{\bf r} \left[ \varepsilon_0 \mathbf{E}_\perp^2 + \mu_0^{-1} \mathbf{B}^2\right]$$ (3.10)

$$H(t) = \sum_n \frac{1}{2m_n} \left[ {\bf p}_n - q_n \mathbf{A}({\bf r}_n,t)\right] + V_{\rm Coul},\quad \div\mathbf{A}=0.$$ (3.11)

without the polarization terms $V_{\bf EP}$ and $V_{\bf gg}$.