




Next: Some Remarks on Fields
Up: Gauge invariance for many
Previous: Coulomb Gauge
Contents
Index
One can now show that the Coulomb gauge Hamiltonian
 can be transformed into a Hamiltonian
can be transformed into a Hamiltonian
 in any other gauge as specified by
in any other gauge as specified by
 and given by Eq. (VII.3.8). This is achieved by the so-called Power-Zienau-Woolley Transformation which is a unitary transformation of the Coulomb gauge Hamiltonian
and given by Eq. (VII.3.8). This is achieved by the so-called Power-Zienau-Woolley Transformation which is a unitary transformation of the Coulomb gauge Hamiltonian
 ,
,
![$\displaystyle {\mathcal H}(t) = \Lambda^{-1} {\mathcal H}_{\rm Coul} (t)\Lambda...
...da \equiv \exp \left[i \int d{\bf r} \mathbf{A}({\bf r},t) \P({\bf r}) \right].$](img1327.png) |
|
|
(3.12) |
A relation can be derived between
 and
and
 , cf. Woolley [8],
, cf. Woolley [8],
 |
|
|
(3.13) |
If this is inserted into
 , Eq. (VII.3.8), one obtains
, Eq. (VII.3.8), one obtains
 |
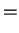 |
 |
|
 |
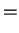 |
![$\displaystyle \frac{1}{2}\int d{\bf r} \left[ \varepsilon_0 \mathbf{E}_\perp^2 + \mu_0^{-1} \mathbf{B}^2\right]$](img1311.png) |
(3.14) |
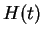 |
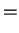 |
 magnetic terms magnetic terms |
|
 |
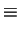 |
 |
|
 |
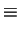 |
 |
|
 |
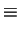 |
 |
(3.15) |
Basically, apart from the magnetic terms the
 coupling is transformed away and one has instead a coupling not to the vector potential, but to the electric field
coupling is transformed away and one has instead a coupling not to the vector potential, but to the electric field
 .
As a slight warning, here things can again get a little bit confusing: compare the discussion in Cohen-Tannoudji, Dupont-Roc and Grynberg [7], and the lecture notes by K.P. Marzlin, http://qis.ucalgary.ca/ pmarzlin/lectures/al0203/ who gives more detailed derivations. In fact, one has to interpret the field in the transformed Hamiltonian as a displacement field
.
As a slight warning, here things can again get a little bit confusing: compare the discussion in Cohen-Tannoudji, Dupont-Roc and Grynberg [7], and the lecture notes by K.P. Marzlin, http://qis.ucalgary.ca/ pmarzlin/lectures/al0203/ who gives more detailed derivations. In fact, one has to interpret the field in the transformed Hamiltonian as a displacement field
 rather than the electric field
rather than the electric field
 .
.





Next: Some Remarks on Fields
Up: Gauge invariance for many
Previous: Coulomb Gauge
Contents
Index
Tobias Brandes
2005-04-26
![$\displaystyle {\mathcal H}(t) = \Lambda^{-1} {\mathcal H}_{\rm Coul} (t)\Lambda...
...da \equiv \exp \left[i \int d{\bf r} \mathbf{A}({\bf r},t) \P({\bf r}) \right].$](img1327.png)
![$\displaystyle {\mathcal H}(t) = \Lambda^{-1} {\mathcal H}_{\rm Coul} (t)\Lambda...
...da \equiv \exp \left[i \int d{\bf r} \mathbf{A}({\bf r},t) \P({\bf r}) \right].$](img1327.png)

![$\displaystyle \frac{1}{2}\int d{\bf r} \left[ \varepsilon_0 \mathbf{E}_\perp^2 + \mu_0^{-1} \mathbf{B}^2\right]$](img1311.png)
 magnetic terms
magnetic terms

