




Next: Harmonic Approximation
Up: Vibrations and Rotations in
Previous: Spin
Contents
Index
Our SE for the radial motion of the two nuclei has the form
![$\displaystyle \left[- \frac{\hbar^2}{2\mu} \left(\frac{\partial^2}{\partial r^2...
...U_\alpha(r)\right] R_{\alpha;Kv}(r) = \varepsilon_{\alpha;Kv} R_{\alpha;Kv}(r).$](img1402.png) |
|
|
(1.26) |
We therefore have two sets of quantum numbers
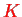 and
and
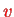 that describe the rotational and vibrational and state of the molecule for a given electronic state
that describe the rotational and vibrational and state of the molecule for a given electronic state
 . Setting
. Setting
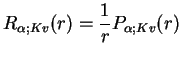 |
|
|
(1.27) |
leads to a standard one-dimensional SE with a `proper'
 kinetic energy term,
kinetic energy term,
![$\displaystyle \left[ -\frac{1}{2\mu}\frac{d^2}{dr^2} + U_\alpha(r) + \frac{K(K+...
...ight] P_{\alpha;Kv}(r)
= \varepsilon_{\alpha;Kv}P_{\alpha;Kv}(r), \quad r\ge 0.$](img1405.png) |
|
|
(1.28) |
Subsections
Tobias Brandes
2005-04-26
![$\displaystyle \left[- \frac{\hbar^2}{2\mu} \left(\frac{\partial^2}{\partial r^2...
...U_\alpha(r)\right] R_{\alpha;Kv}(r) = \varepsilon_{\alpha;Kv} R_{\alpha;Kv}(r).$](img1402.png)
![$\displaystyle \left[- \frac{\hbar^2}{2\mu} \left(\frac{\partial^2}{\partial r^2...
...U_\alpha(r)\right] R_{\alpha;Kv}(r) = \varepsilon_{\alpha;Kv} R_{\alpha;Kv}(r).$](img1402.png)
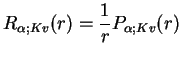
![$\displaystyle \left[ -\frac{1}{2\mu}\frac{d^2}{dr^2} + U_\alpha(r) + \frac{K(K+...
...ight] P_{\alpha;Kv}(r)
= \varepsilon_{\alpha;Kv}P_{\alpha;Kv}(r), \quad r\ge 0.$](img1405.png)