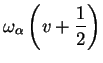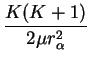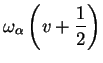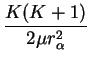Next: Spin
Up: Radial SE
Previous: Harmonic Approximation
Contents
Index
The structure of the energy spectrum is determined by the magnitude of the three terms
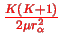 ,
,
 , and
, and
 . These differ strongly due to their dependence on the relative nuclei mass
. These differ strongly due to their dependence on the relative nuclei mass
 . In terms of the small dimensionless parameter
. In terms of the small dimensionless parameter
 (where
(where
 is the electron mass), we have
is the electron mass), we have
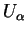 |
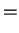 |
 electronic part electronic part |
(1.32) |
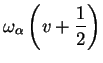 |
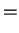 |
 vibrational part vibrational part |
(1.33) |
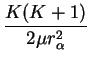 |
 |
 rotational part rotational part |
(1.34) |
In spectroscopic experiments, one determined energy differences
 which therefore are broadly determined by
which therefore are broadly determined by
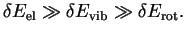 |
|
|
(1.35) |





Next: Spin
Up: Radial SE
Previous: Harmonic Approximation
Contents
Index
Tobias Brandes
2005-04-26